Chapter 58 Estimating Structural Regression Models Using Structural Equation Modeling

In this chapter, we will learn how to estimate structural regression models, which are part of the structural equation modeling (SEM) family of analyses. Specifically, we will learn how to integrate the measurement model and structural model into a single SEM.

58.1 Conceptual Overview

Structural equation modeling (SEM) is a latent variable modeling approach that can be used to estimate confirmatory factor analysis models, latent growth models, latent change score models, and structural regression models. We can also use SEM to simultaneously estimate multiple relations between observed variables by implementing path analysis model.

In this chapter, we will focus on estimating structural regression models (SRM), which is often what comes to mind when people think of SEM. An SRM allows us to integrate our measurement model (via confirmatory factor analysis) and structural model (i.e., direct relations, indirect relations). In doing so, when estimating direct and indirect relations involving latent factors, we can account for measurement error (e.g., unreliability) in the observed variables (e.g., multiple items) that serve as indicators of those latent factors.

58.1.1 Path Diagrams

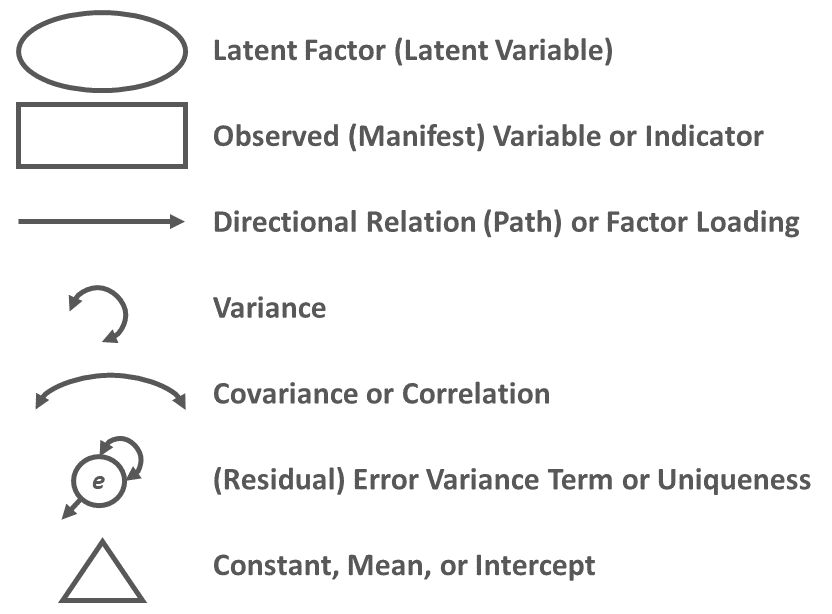
It is often helpful to visualize an SRM using a path diagram. A path diagram displays the model parameter specifications and can also include parameter estimates. Conventional path diagram symbols are shown in Figure 1.

Figure 1: Conventional path diagram symbols and their meanings.

For an example of how the path diagram symbols can be used to construct a visual depiction of an SRM, please reference Figure 2. The path diagram depicts an SRM with four latent factors (i.e., role clarity, task mastery, job satisfaction, performance), their respective measurement structures, and their structural relations with each other.

Figure 2: Example of structural regression model path diagram.

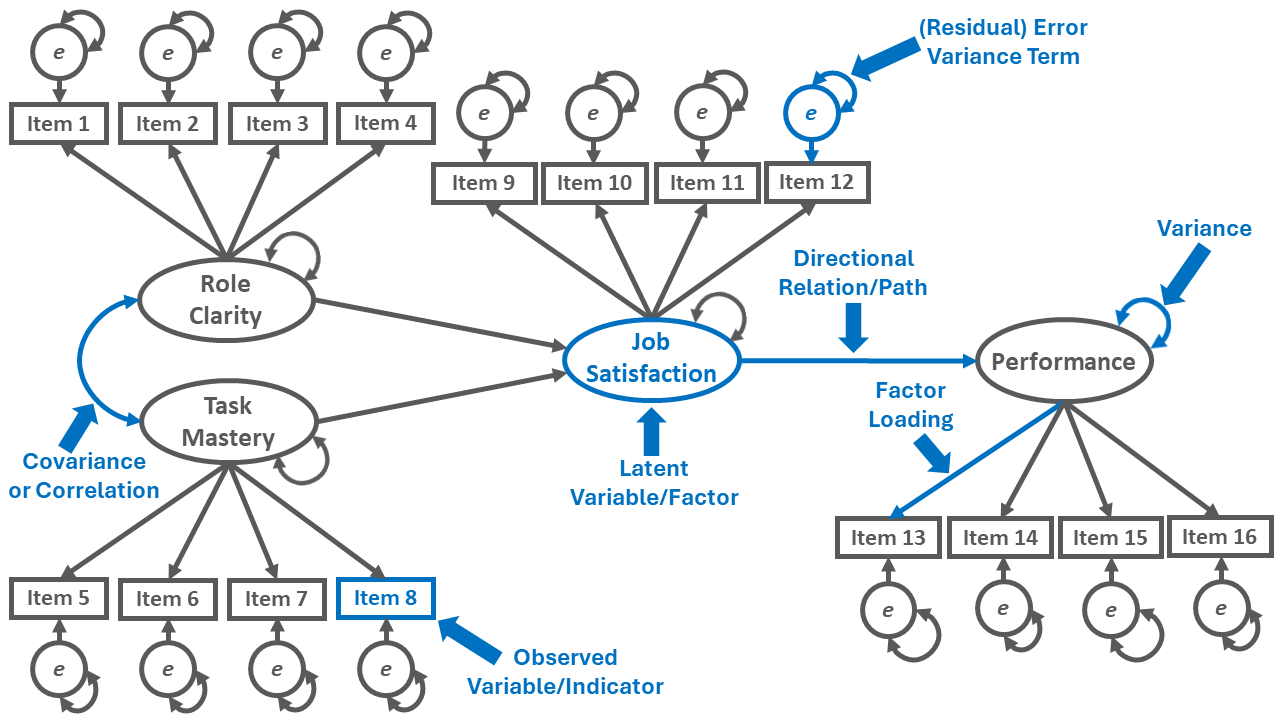
By convention, the latent factors are represented by an oval or circle. Please note that the latent factor is not directly measured; rather, we infer information about each latent factor based on its indicators (i.e., observed variables), which in this example correspond to the items loading on the latent factor.

Latent factors have variance terms associated with them, which represent the latent factors’ variabilities; these variances terms, which are represented by double-headed arrows, reflect the extent to which the latent factor estimates vary between individuals.

A bidirectional association between latent factors is depicted with the double-headed arrow, which is referred to as a covariance – or if standardized, a correlation.

Each observed variable (indicator) is represented with a rectangle. A one-directional, single-sided arrow extending from a latent factor to an observed variable represents a factor loading.

Each observed variable has a (residual) error variance term, which represents the amount of variance left unexplained by the latent factor in relation to the observed variable.

A directional relation (path) from one latent factor to another is represented by a single-headed arrow, and represents a regression. Directional relations are often of most substantive interest in an SRM and often corresponding to formal hypotheses or questions that we are attempting to test or answer.

58.1.2 Model Identification

Model identification has to do with the number of (free or freely estimated) parameters specified in the model relative to the number of unique (non-redundant) sources of information available, and model implication has important implications for assessing model fit and estimating parameter estimates.

Just-identified: In a just-identified model (i.e., saturated model), the number of freely estimated parameters (e.g., factor loadings, covariances, variances) is equal to the number of unique (non-redundant) sources of information, which means that the degrees of freedom (df) is equal to zero. In just-identified models, the model parameter standard errors can be estimated, but the model fit cannot be assessed in a meaningful way using traditional model fit indices.

Over-identified: In an over-identified model, the number of freely estimated parameters is less than the number of unique (non-redundant) sources of information, which means that the degrees of freedom (df) is greater than zero. In over-identified models, traditional model fit indices and parameter standard errors can be estimated.

Under-identified: In an under-identified model, the number of freely estimated parameters is greater than the number of unique (non-redundant) sources of information, which means that the degrees of freedom (df) is less than zero. In under-identified models, the model parameter standard errors and model fit cannot be estimated. Some might say under-identified models are overparameterized because they have more parameters to be estimated than unique sources of information.

Most (if not all) statistical software packages that allow structural equation modeling (and by extension, SRM) automatically compute the degrees of freedom for a model or, if the model is under-identified, provide an error message. As such, we don’t need to count the number of sources of unique (non-redundant) sources of information and free parameters by hand. With that said, to understand model identification and its various forms at a deeper level, it is often helpful to practice calculating the degrees freedom by hand when first learning.

The formula for calculating the number of unique (non-redundant) sources of information available for a particular model is as follows:

\(i = \frac{p(p+1)}{2}\)

where \(p\) is the number of observed variables to be modeled. This formula calculates the number of possible unique covariances and variances for the variables specified in the model – or in other words, it calculates the lower diagonal of a covariance matrix, including the variances.

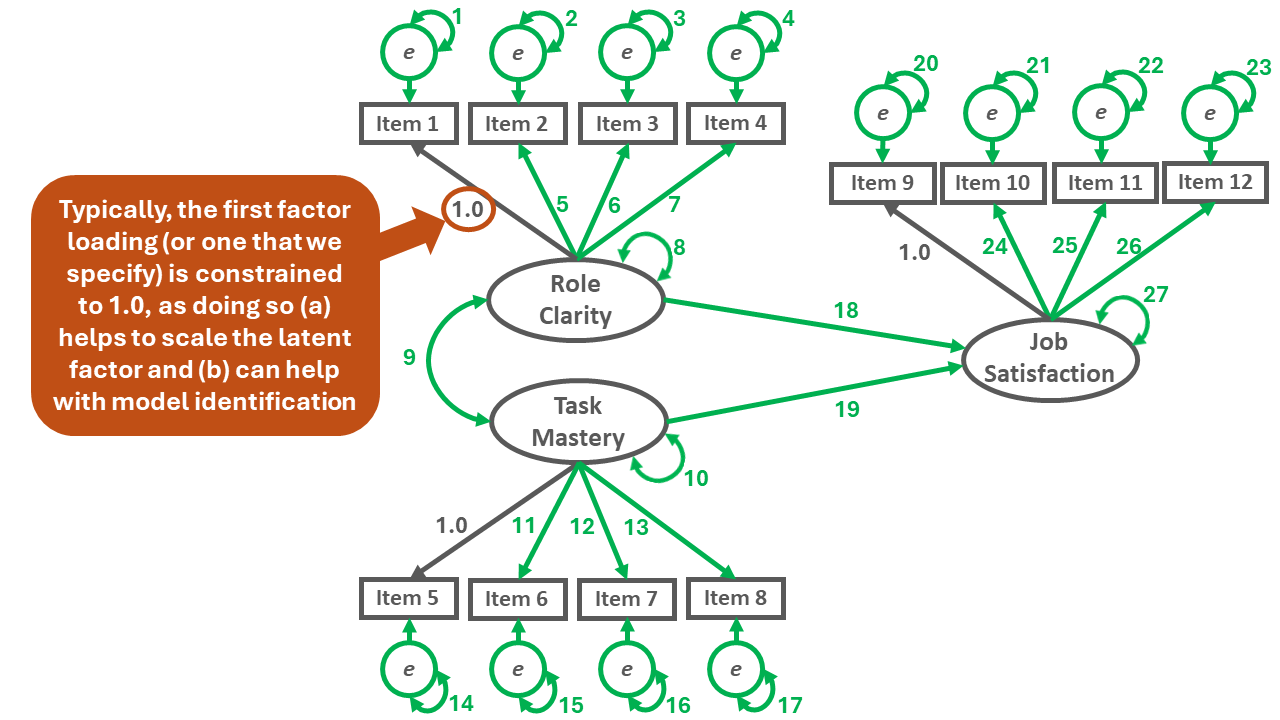
In the SRM shown in Figure 3 below, there are 12 observed variables: Items 1-12. Accordingly, in the following formula, \(p\) is equal to 12, and the number of unique (non-redundant) sources of information is 78.

\(i = \frac{12(12+1)}{2} = \frac{156}{2} = 78\)

To count the number of free parameters (\(k\)), simply add up the number of the specified unconstrained (freely estimated) factor loadings, variances, covariances, directional relations, and (residual) error variance terms in the SRM. Please note that for latent variable scaling and model identification purposes, for each latent factor, we typically constrain one of the factor loadings to 1.0, which means that it is not freely estimated and thus doesn’t count as one of the free parameters. The example SRM shown in Figure 3 has 27 free parameters.

\(k = 27\)

To calculate the degrees of freedom (df) for the model, we need to subtract the number of free parameters from the number unique (non-redundant) sources of information, which in this example equates to 78 minus 28. Thus, the degrees of freedom for the model is 50, which means the model is over-identified.

\(df = i - k = 78 - 27 = 51\)

Figure 3: Counting the number of free parameters in the SRM path diagram.

58.1.3 Model Fit

When a model is over-identified (df > 0), the extent to which the specified model fits the data can be assessed using a variety of model fit indices, such as the chi-square (\(\chi^{2}\)) test, comparative fit index (CFI), Tucker-Lewis index (TLI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR). For a commonly cited reference on cutoffs for fit indices, please refer to Hu and Bentler (1999), and for a concise description of common guidelines regarding interpreting model fit indices, including differences between stringent and relaxed interpretations of common fit indices, I recommend checking out Nye (2023). With that being said, those papers focus on confirmatory factor analyses as opposed to SRM, but confirmatory factor analyses are integrated into SRM, so they still have some relevance. Regardless of which cutoffs we apply when interpreting fit indices, we must remember that such cutoffs are merely guidelines, and it’s possible to estimate an acceptable model that meets some but not all of the cutoffs given the limitations of some fit indices. Further, in light of the limitations of conventional model fit index cutoffs, McNeish and Wolf (2023) developed model- and data-specific dynamic fit index cutoffs, which we will cover later in the chapter tutorial.

Chi-square test. The chi-square (\(\chi^{2}\)) test can be used to assess whether the model fits the data adequately, where a statistically significant \(\chi^{2}\) value (e.g., p \(<\) .05) indicates that the model does not fit the data well and a nonsignificant chi-square value (e.g., p \(\ge\) .05) indicates that the model fits the data reasonably well (Bagozzi and Yi 1988). The null hypothesis for the \(\chi^{2}\) test is that the model fits the data perfectly, and thus failing to reject the null model provides some confidence that the model fits the data reasonably close to perfectly. Of note, the \(\chi^{2}\) test is sensitive to sample size and non-normal variable distributions.

Comparative fit index (CFI). As the name implies, the comparative fit index (CFI) is a type of comparative (or incremental) fit index, which means that CFI compares the focal model to a baseline model, which is commonly referred to as the null or independence model. CFI is generally less sensitive to sample size than the chi-square test. A CFI value greater than or equal to .95 generally indicates good model fit to the data, although some might relax that cutoff to .90.

Tucker-Lewis index (TLI). Like CFI, Tucker-Lewis index (TLI) is another type of comparative (or incremental) fit index. TLI is generally less sensitive to sample size than the chi-square test and tends to work well with smaller sample sizes; however, as Hu and Bentler (1999) noted, TLI may be not be the best choice for smaller sample sizes (e.g., N \(<\) 250). A TLI value greater than or equal to .95 generally indicates good model fit to the data, although some might relax that cutoff to .90.

Root mean square error of approximation (RMSEA). The root mean square error of approximation (RMSEA) is an absolute fit index that penalizes model complexity (e.g., models with a larger number of estimated parameters) and thus ends up effectively rewarding more parsimonious models. RMSEA values tend to upwardly biased when the model degrees of freedom are fewer (i.e., when the model is closer to being just-identified); further, Hu and Bentler (1999) noted that RMSEA may not be the best choice for smaller sample sizes (e.g., N \(<\) 250). In general, an RMSEA value that is less than or equal to .06 indicates good model fit to the data, although some relax that cutoff to .08 or even .10.

Standardized root mean square residual (SRMR). Like the RMSEA, the standardized root mean square residual (SRMR) is an example of an absolute fit index. An SRMR value that is less than or equal to .06 generally indicates good fit to the data, although some relax that cutoff to .08.

Summary of model fit indices. The conventional cutoffs for the aforementioned model fit indices – like any rule of thumb – should be applied with caution and with good judgment and intention. Further, these indices don’t always agree with one another, which means that we often look across multiple fit indices and come up with our best judgment of whether the model adequately fits the data. A poorly fitting model may be due to model misspecification, an inappropriate model estimator, a large amount of error around slope estimates, or other factors that need to be addressed. With that being said, we should also be careful to not toss out a model entirely if one or more of the model fit indices suggest less than acceptable levels of fit to the data. The table below contains the conventional stringent and more relaxed cutoffs for the model fit indices.

Fit Index	Stringent Cutoffs for Acceptable Fit	Relaxed Cutoffs for Acceptable Fit
\(\chi^{2}\)	\(p \ge .05\)	\(p \ge .01\)
CFI	\(\ge .95\)	\(\ge .90\)
TLI	\(\ge .95\)	\(\ge .90\)
RMSEA	\(\le .06\)	\(\le .08\)
SRMR	\(\le .06\)	\(\le .08\)

58.1.4 Parameter Estimates

In SRM, there are various types of parameter estimates, which correspond to the path diagram symbols covered earlier (e.g., covariance, variance, mean, factor loading). When a model is just-identified or over-identified, we can estimate the standard errors for freely estimated parameters, which allows us to evaluate statistical significance. With most software applications, we can request standardized parameter estimates, which can facilitate the interpretation of some parameters.

Factor loadings. When we standardize factor loadings, we obtain estimates for each directional relation between the latent factor and an indicator, including for the factor loading that we likely constrained to 1.0 for latent factor scaling and model identification purposes (see above). When standardized, factor loadings can be interpreted like correlations, and generally we want to see standardized estimate values between .50 and .95 (Bagozzi and Yi 1988). If a standardized factor loading falls outside of that range, we typically investigate whether there is a theoretical or empirical reason for the out-of-range estimate, and we may consider removing the associated indicator if warranted.

Variances. The variance estimate of the latent factor is generally not a focus when evaluating parameter estimates in an SRM, as the variance of a latent factor depends on the factor loadings and scaling.

Covariances. In an SRM, covariances between latent factors help us understand the extent to which they are related (or unrelated). When standardized, a covariance can be interpreted as a correlation.

Directional paths. Directional paths can be between two latent factors, between two observed variables, or between a latent factor and an observed variable. Directional paths represent structural components of an SRM and can be thought of as regressions. Further, they are often tied to hypotheses or research questions, meaning that we tend to focus on their statistical significance and practical significance.

(Residual) error variance terms. The (residual) error variance terms, which are also known as disturbance terms or uniquenesses, indicate how much variance is left unexplained by the latent factor in relation to the indicators. When standardized, error variance terms represent the proportion (percentage) of variance that remains unexplained by the latent factor. Ideally, we want to see standardized error variance terms that are less than or equal to .50.

58.1.5 Model Comparisons

When evaluating an SRM, we often wish to evaluate whether the focal model performs better (or worse) than an alternative model. Comparing models can help us arrive at a more parsimonious model that still fits the data well.

As an example, imagine our focal model is the one shown in Figure 2 above. Now imagine that we specify an alternative model that has two extra freely estimated directional paths from Role Clarity to Performance and from Task Mastery to Performance. We can compare those two models to determine whether our focal model fits the data about as well as or worse than the less parsimonious alternative model with two extra directional paths.

When two models are nested, we can perform nested model comparisons. As a reminder, a nested model has all the same parameter estimates of a full model but has additional parameter constraints in place. If two models are nested, we can compare them using model fit indices like CFI, TLI, RMSEA, and SRMR. We can also use the chi-square difference (\(\Delta \chi^{2}\)) test (likelihood ratio test) to compare nested models, which provides a statistical test for nested-model comparisons.

When two models are not nested, we can use other model fit indices like Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). With respect to these indices, the best fitting model will have lower AIC and BIC values.

58.1.6 Statistical Assumptions

The statistical assumptions that should be met prior to estimating and/or interpreting an SRM will depend on the type of estimation method. Common estimation methods for SRM models include (but are not limited to) maximum likelihood (ML), maximum likelihood with robust standard errors (MLM or MLR), weighted least squares (WLS), and diagonally weighted least squares (DWLS). WLS and DWLS estimation methods are used when there are observed variables with nominal or ordinal (categorical) measurement scales. In this chapter, we will focus on ML estimation, which is a common method when observed variables have interval or ratio (continuous) measurement scales. As Kline (2011) notes, ML estimation carries with it the following assumptions: “The statistical assumptions of ML estimation include independence of the scores, multivariate normality of the endogenous variables, and independence of the exogenous variables and error terms” (p. 159). When multivariate non-normality is a concern, the MLM or MLR estimator is a better choice than ML estimator, where the MLR estimator allows for missing data and the MLM estimator does not.

58.1.6.1 Sample Write-Up

After their respective start dates, we assessed 550 new employees’ role clarity (1 month post-hire), task mastery (1 month post-hire), job satisfaction (6 months post-hire), and supervisor-rated job satisfaction (6 months post-hire); missing data were not a concern. Each construct’s associated multi-item measure included four items. We hypothesized that higher role clarity and task mastery is associated with higher job satisfaction, and that higher job satisfaction is associated with higher job performance. Before estimating a structural regression model to test those hypotheses, we evaluated the measurement structure of the four measures using a multi-factor confirmatory factor analysis model. We evaluated the model’s fit to the data using the chi-square (\(\chi^{2}\)) test, CFI, TLI, RMSEA, and SRMR model fit indices. The \(\chi^{2}\) test indicated that the model fit the data as well as a perfectly fitting model (\(\chi^{2}\) = 120.274 df = 98, p = .063). Further, the CFI and TLI estimates were .994 and .993, respectively, which exceeded the more stringent threshold of .95, thereby indicating that model showed acceptable fit to the data. Similarly, the RMSEA estimate was .020, which was below the more stringent threshold of .06, thereby indicating that model showed acceptable fit to the data. The SRMR estimate was .024, which was below the stringent threshold of .06, thereby indicating acceptable model fit to the data. Collectively, the model fit information indicated that the four-factor measurement model fit the data acceptably. Further, standardized factor loadings ranged from .682 to .802, which all fell well within the recommended .50-.95 acceptability range. The standardized error variances for items ranged from .358 to .534, and only one estimate associated with the first role clarity item was above the the target threshold of .50, thereby indicating that it was unlikely that an unmodeled construct had an outsized influence on the items. The average variance extracted (AVE) estimates for role clarity, task mastery, job satisfaction, and job performance were .546, .608, .567, and .606, respectively, which all exceeded the .50 cutoff; thus, all four latent factors showed acceptable AVE levels. The composite reliability (CR) estimates for role clarity, task mastery, job satisfaction, and job performance were were .827, .861, .840, and .860, and all indicated acceptable levels of internal consistency reliability. In sum, the updated four-factor measurement model also showed acceptable fit to the data and acceptable parameter estimates, acceptable AVE estimates, and acceptable CR estimates.

Using the four-factor measurement model, we proceeded with estimating a structural regression model to test our hypotheses. The \(\chi^{2}\) test indicated that the model fit the data as well as a perfectly fitting model (\(\chi^{2}\) = 120.858 df = 100, p = .076). Further, the CFI and TLI estimates were .994 and .993, respectively, which exceeded the more stringent threshold of .95, thereby indicating that model showed acceptable fit to the data. Similarly, the RMSEA estimate was .019, which was below the more stringent threshold of .06, thereby indicating that model showed acceptable fit to the data. The SRMR estimate was .025, which was below the stringent threshold of .06, thereby indicating acceptable model fit to the data. Collectively, the model fit information indicated that the SRM fit the data acceptably. As hypothesized, the standardized directional path from: (a) role clarity to job satisfaction was statistically significant and positive (.356, p < .001); (b) from task mastery to job satisfaction was statistically significant and positive (.300, p < .001); and (c) from job satisfaction to job performance was statistically significant and positive (.389, p < .001).

58.2 Tutorial

This chapter’s tutorial demonstrates how to estimate structural regression models using structural equation modeling in R.

58.2.1 Video Tutorial

The video tutorial for this chapter is planned but has not yet been recorded.

58.2.2 Functions & Packages Introduced

Function	Package
cfa	lavaan
summary	base R
AVE	semTools
compRelSEM	semTools
semPaths	semPlot
sem	lavaan
anova	base R
options	base R
parameterEstimates	lavaan
inspect	lavaan
cbind	base R
rbind	base R
t	base R
ampute	mice

58.2.3 Initial Steps

If you haven’t already, save the file called “sem.csv” into a folder that you will subsequently set as your working directory. Your working directory will likely be different than the one shown below (i.e., "H:/RWorkshop"). As a reminder, you can access all of the data files referenced in this book by downloading them as a compressed (zipped) folder from the my GitHub site: https://github.com/davidcaughlin/R-Tutorial-Data-Files; once you’ve followed the link to GitHub, just click “Code” (or “Download”) followed by “Download ZIP”, which will download all of the data files referenced in this book. For the sake of parsimony, I recommend downloading all of the data files into the same folder on your computer, which will allow you to set that same folder as your working directory for each of the chapters in this book.

Next, using the setwd function, set your working directory to the folder in which you saved the data file for this chapter. Alternatively, you can manually set your working directory folder in your drop-down menus by going to Session > Set Working Directory > Choose Directory…. Be sure to create a new R script file (.R) or update an existing R script file so that you can save your script and annotations. If you need refreshers on how to set your working directory and how to create and save an R script, please refer to Setting a Working Directory and Creating & Saving an R Script.

# Set your working directory
setwd("H:/RWorkshop")

Next, read in the .csv data file called “sem.csv” using your choice of read function. In this example, I use the read_csv function from the readr package (Wickham, Hester, and Bryan 2024). If you choose to use the read_csv function, be sure that you have installed and accessed the readr package using the install.packages and library functions. Note: You don’t need to install a package every time you wish to access it; in general, I would recommend updating a package installation once ever 1-3 months. For refreshers on installing packages and reading data into R, please refer to Packages and Reading Data into R.

# Install readr package if you haven't already
# [Note: You don't need to install a package every 
# time you wish to access it]
install.packages("readr")

# Access readr package
library(readr)

# Read data and name data frame (tibble) object
df <- read_csv("sem.csv")

# Print the names of the variables in the data frame (tibble) object
names(df)

##  [1] "EmployeeID" "RC1"        "RC2"        "RC3"        "RC4"        "TM1"        "TM2"        "TM3"        "TM4"       
## [10] "JS1"        "JS2"        "JS3"        "JS4"        "JP1"        "JP2"        "JP3"        "JP4"        "Gender"

# Print number of rows in data frame (tibble) object
nrow(df)

## [1] 550

# Print top 6 rows of data frame (tibble) object
head(df)

## # A tibble: 6 × 18
##   EmployeeID   RC1   RC2   RC3   RC4   TM1   TM2   TM3   TM4   JS1   JS2   JS3   JS4   JP1   JP2   JP3   JP4 Gender
##   <chr>      <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl>
## 1 EE1001         4     4     3     4     3     4     5     4     2     3     4     4     6     7     7     7      1
## 2 EE1002         5     4     3     6     5     6     5     5     5     3     5     3     7     6     6     7      1
## 3 EE1003         4     4     5     2     3     4     4     5     5     5     5     6     7     9     7     7      0
## 4 EE1004         5     4     5     5     2     3     3     4     3     4     4     3     8     8     8    10      0
## 5 EE1005         2     3     2     2     2     3     3     1     3     3     2     4     6     6     7     6      1
## 6 EE1006         4     5     5     3     3     2     4     2     5     4     5     3     6     7     6     6      0

The data frame includes data from a new-employee onboarding survey administered 1-month after employees’ respective start dates, an engagement survey administered 6 months after employees’ respective start dates, and a supervisor-rated job performance measure administered 12 months after employees’ respective start dates. The sample includes 550 employees, and the data have already been joined for you. In total, employees responded to four multi-item measures: role clarity (1 month), task mastery (1 month), job satisfaction (6 months), and job performance (12 months). As part of initial survey, employees employees self-reported their gender identities (Gender). Employees responded to items from the role clarity, task mastery, and job satisfaction measures using a 7-point agreement Likert-type response format, ranging from Strongly Disagree (1) to Strongly Agree (7). Employees’ supervisors responded to items from the supervisor-rated job performance measure using a 10-point response format, ranging from Does Not Meet Expectations (1) to Exceeds Expectations (10). For all items, higher scores indicate higher levels of the construct being measured.

The first multi-item measure is employee-rated and is designed to measure role clarity, which is conceptually defined as “the extent to which an individual understands what is expected of them in their job or role.” The measure includes the following four items.

• RC1 (“I understand what my job-related responsibilities are.”)

• RC2 (“I understand what the organization expects of me in my job.”)

• RC3 (“My job responsibilities have been clearly communicated to me.”)

• RC4 (“My role in the organization is clear to me.”)

The second multi-item measure is employee-rated and is designed to measure task mastery, which is conceptually defined as “the extent to which an individual feels self-efficacious in their role and feels confident in performing their job responsibilities.” The measure includes the following four items.

• TM1 (“I am confident I can perform my job responsibilities effectively.”)

• TM2 (“I am able to address unforeseen job-related challenges.”)

• TM3 (“When I apply effort at work, I perform well.”)

• TM4 (“I am proficient in the skills needed to perform my job.”)

The third multi-item measure is employee-rated and is designed to measure job satisfaction, which is conceptually defined as “the extent to which an individual favorably evaluates their job and components of their job.” The measure includes the following four items.

• JS1 (“In general, I am satisfied with my job.”)

• JS2 (“I enjoy completing my work tasks.”)

• JS3 (“I like all aspects of my job.”)

• JS4 (“It is a pleasure to fulfill my job responsibilities.”)

The fourth multi-item measure is supervisor-rated and is designed to measure employees’ job performance, which is conceptually defined as “the extent to which an individual effectively fulfills their tasks, duties, and responsibilities.” The measure includes the following four items.

• JP1 (“This employee completes administrative tasks successfully.”)

• JP2 (“This employee provides high-quality service to customers.”)

• JP3 (“This employee collaborates effectively with team members.”)

• JP4 (“This employee applies rigorous problem solving on the job.”)

58.2.4 Evaluate the Measurement Model Using Confirmatory Factor Analysis

Prior to estimating a structural regression model (SRM), it is customary to evaluate the measurement model using confirmatory factor analysis (CFA). More specifically, we will be estimating a multi-factor CFA because we have four multi-item measures of interest. Doing so allows us to evaluate the latent factor structure and whether our empirical evidence supports the theoretically distinguishable constructs we attempted to measure; in other words, multi-factor CFA models are useful for evaluating whether theoretically distinguishable constructs are in fact empirically distinguishable based on the acquired data. Because an earlier chapter provides an in-depth introduction to CFA, for the most part, we will breeze through evaluating the measurement model in this chapter. If you need a refresher on CFA, please check out that earlier chapter.

As a reminder, our data frame (df) includes responses to four multi-item measures: role clarity (1 month post-hire), task mastery (1 month post-hire), job satisfaction (6 months post-hire), and supervisor-rated job satisfaction (6 months post-hire). In this section we will specify a four-factor CFA model with four latent factors corresponding to role clarity, task mastery, job satisfaction, and job performance, with each measure’s items loading on its respective latent factor. In doing so, we can determine whether this four-factor model fits the data acceptably.

First, because CFA is a specific application of structural equation modeling (SEM), we will use functions from an R package developed for SEM called lavaan (latent variable analysis) to estimate our CFA model. If you haven’t already, begin by installing and accessing the lavaan package.

# Install package
install.packages("lavaan")

# Access package
library(lavaan)

Second, we will specify a four-factor CFA model and assign it to an object that we can subsequently reference. To do so, we will do the following.

1. Specify a name for the model object (e.g., cfa_mod), followed by the <- assignment operator.
2. To the right of the <- assignment operator and within quotation marks (" "):
   • Specify a name for the role clarity latent factor (e.g., RC), followed by the =~ operator, which is used to indicate how a latent factor is measured. Anything that comes to the right of the =~ operator is an indicator (e.g., item) of the latent factor. Please note that the latent factor is not something that we directly observe, so it will not have a corresponding variable in our data frame object. After the =~ operator, specify each indicator (i.e., item) associated with the latent factor, and to separate the indicators, insert the + operator. In this example, the four indicators of the role clarity latent factor (RC) are: RC1 + RC2 + RC3 + RC4. These are our observed variables, which conceptually are influenced by the underlying latent factor.
   • Repeat the previous step for the task mastery (e.g., TM), job satisfaction (e.g., JS), and job performance (e.g., JP) latent factors.

# Specify four-factor CFA model & assign to object
cfa_mod <- "
RC =~ RC1 + RC2 + RC3 + RC4
TM =~ TM1 + TM2 + TM3 + TM4
JS =~ JS1 + JS2 + JS3 + JS4
JP =~ JP1 + JP2 + JP3 + JP4
"

Third, now that we have specified the model object (cfa_mod), we are ready to estimate the model using the cfa function from the lavaan package. To do so, we will do the following.

1. Specify a name for the fitted model object (e.g., cfa_fit), followed by the <- assignment operator.
2. To the right of the <- assignment operator, type the name of the cfa function, and within the function parentheses include the following arguments.
   • As the first argument, insert the name of the model object that we specified above (cfa_mod).
   • As the second argument, insert the name of the data frame object to which the indicator variables in our model belong. That is, after data=, insert the name of the data frame object (df).
   • Note: The cfa function includes model estimation defaults, which explains why we had relatively few model specifications. For example, the function defaults to constraining the first indicator’s unstandardized factor loading to 1.0 for model fitting purposes, and constrains covariances between indicator error terms (i.e., uniquenesses) to zero (or in other words, specifies the error terms as uncorrelated).

# Estimate four-factor CFA model & assign to fitted model object
cfa_fit <- cfa(cfa_mod,      # name of specified model object
               data=df)      # name of data frame object

Fourth, we will use the summary function from base R to to print the model results. To do so, we will apply the following arguments in the summary function parentheses.

1. As the first argument, specify the name of the fitted model object that we created above (cfa_fit).
2. As the second argument, set fit.measures=TRUE to obtain the model fit indices (e.g., CFI, TLI, RMSEA, SRMR).
3. As the third argument, set standardized=TRUE to request the standardized parameter estimates for the model.

# Print summary of model results
summary(cfa_fit,             # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE)   # request standardized estimates

## lavaan 0.6.15 ended normally after 36 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        38
## 
##   Number of observations                           550
## 
## Model Test User Model:
##                                                       
##   Test statistic                               120.274
##   Degrees of freedom                                98
##   P-value (Chi-square)                           0.063
## 
## Model Test Baseline Model:
## 
##   Test statistic                              3851.181
##   Degrees of freedom                               120
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.994
##   Tucker-Lewis Index (TLI)                       0.993
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -12611.728
##   Loglikelihood unrestricted model (H1)     -12551.591
##                                                       
##   Akaike (AIC)                               25299.456
##   Bayesian (BIC)                             25463.233
##   Sample-size adjusted Bayesian (SABIC)      25342.605
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.020
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.032
##   P-value H_0: RMSEA <= 0.050                    1.000
##   P-value H_0: RMSEA >= 0.080                    0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.024
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC =~                                                                 
##     RC1               1.000                               0.746    0.682
##     RC2               1.213    0.080   15.227    0.000    0.905    0.801
##     RC3               1.038    0.073   14.127    0.000    0.774    0.716
##     RC4               1.110    0.076   14.587    0.000    0.828    0.747
##   TM =~                                                                 
##     TM1               1.000                               0.923    0.783
##     TM2               1.051    0.058   18.231    0.000    0.970    0.783
##     TM3               0.998    0.054   18.646    0.000    0.921    0.802
##     TM4               0.985    0.056   17.521    0.000    0.909    0.753
##   JS =~                                                                 
##     JS1               1.000                               0.908    0.737
##     JS2               1.048    0.063   16.585    0.000    0.951    0.777
##     JS3               0.994    0.063   15.793    0.000    0.902    0.734
##     JS4               1.033    0.063   16.368    0.000    0.937    0.764
##   JP =~                                                                 
##     JP1               1.000                               1.168    0.766
##     JP2               1.103    0.061   18.202    0.000    1.289    0.801
##     JP3               0.980    0.054   18.031    0.000    1.145    0.793
##     JP4               0.994    0.058   17.123    0.000    1.161    0.752
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC ~~                                                                 
##     TM                0.087    0.035    2.478    0.013    0.127    0.127
##     JS                0.266    0.040    6.665    0.000    0.392    0.392
##     JP                0.148    0.045    3.273    0.001    0.170    0.170
##   TM ~~                                                                 
##     JS                0.287    0.046    6.225    0.000    0.343    0.343
##     JP                0.174    0.055    3.199    0.001    0.162    0.162
##   JS ~~                                                                 
##     JP                0.409    0.060    6.820    0.000    0.386    0.386
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC1               0.639    0.047   13.652    0.000    0.639    0.534
##    .RC2               0.458    0.044   10.494    0.000    0.458    0.359
##    .RC3               0.571    0.044   13.023    0.000    0.571    0.488
##    .RC4               0.545    0.044   12.272    0.000    0.545    0.443
##    .TM1               0.538    0.044   12.283    0.000    0.538    0.387
##    .TM2               0.594    0.048   12.289    0.000    0.594    0.387
##    .TM3               0.472    0.040   11.698    0.000    0.472    0.358
##    .TM4               0.631    0.048   13.049    0.000    0.631    0.433
##    .JS1               0.692    0.053   12.988    0.000    0.692    0.457
##    .JS2               0.596    0.050   11.972    0.000    0.596    0.397
##    .JS3               0.696    0.053   13.053    0.000    0.696    0.461
##    .JS4               0.625    0.051   12.321    0.000    0.625    0.416
##    .JP1               0.961    0.075   12.727    0.000    0.961    0.413
##    .JP2               0.925    0.079   11.682    0.000    0.925    0.358
##    .JP3               0.773    0.065   11.957    0.000    0.773    0.371
##    .JP4               1.035    0.079   13.056    0.000    1.035    0.434
##     RC                0.557    0.066    8.373    0.000    1.000    1.000
##     TM                0.852    0.083   10.305    0.000    1.000    1.000
##     JS                0.824    0.088    9.381    0.000    1.000    1.000
##     JP                1.364    0.137    9.992    0.000    1.000    1.000

Evaluating model fit. Now that we have the summary of our model results, we will begin by evaluating key pieces of the model fit information provided in the output.

• Estimator. The function defaulted to using the maximum likelihood (ML) model estimator. When there are deviations from multivariate normality or categorical variables, the function may switch to another estimator.
• Number of parameters. Thirty-eight parameters were estimated, which as we will see later correspond to factor loadings, covariances, and (residual error) variances.
• Number of observations. Our effective sample size is 550. Had there been missing data on the observed variables, this portion of the output would have indicated how many of the observations were retained for the analysis given the missing data. How missing data are handled during estimation will depend on the type of missing data approach we apply, which is covered in more default in the section called Estimating Models with Missing Data. By default, the cfa function applies listwise deletion in the presence of missing data.
• Chi-square test. The chi-square (\(\chi^{2}\)) test assesses whether the model fits the data adequately, where a statistically significant \(\chi^{2}\) value (e.g., p \(<\) .05) indicates that the model does not fit the data well and a nonsignificant chi-square value (e.g., p \(\ge\) .05) indicates that the model fits the data reasonably well (Bagozzi and Yi 1988). The null hypothesis for the \(\chi^{2}\) test is that the model fits the data perfectly, and thus failing to reject the null model provides some confidence that the model fits the data reasonably close to perfectly. Of note, the \(\chi^{2}\) test is sensitive to sample size and non-normal variable distributions. For this model, we find the \(\chi^{2}\) test in the output section labeled Model Test User Model. Because the p-value is equal to or greater than .05, we fail to reject the null hypothesis that the mode fits the data perfectly and thus conclude that the model fits the data acceptably (\(\chi^{2}\) = 120.274, df = 98, p = .063). Finally, note that because the model’s degrees of freedom (i.e., 98) is greater than zero, we can conclude that the model is over-identified.
• Comparative fit index (CFI). As the name implies, the comparative fit index (CFI) is a type of comparative (or incremental) fit index, which means that CFI compares our estimated model to a baseline model, which is commonly referred to as the null or independence model. CFI is generally less sensitive to sample size than the chi-square (\(\chi^{2}\)) test. A CFI value greater than or equal to .95 generally indicates good model fit to the data, although some might relax that cutoff to .90. For this model, CFI is equal to .994, which indicates that the model fits the data acceptably.
• Tucker-Lewis index (TLI). Like CFI, Tucker-Lewis index (TLI) is another type of comparative (or incremental) fit index. TLI is generally less sensitive to sample size than the chi-square test and tends to work well with smaller sample sizes; however, as Hu and Bentler (1999) noted, TLI may be not be the best choice for smaller sample sizes (e.g., N \(<\) 250). A TLI value greater than or equal to .95 generally indicates good model fit to the data, although like CFI, some might relax that cutoff to .90. For this model, TLI is equal to .993, which indicates that the model fits the data acceptably.
• Loglikelihood and Information Criteria. The section labeled Loglikelihood and Information Criteria contains model fit indices that are not directly interpretable on their own (e.g., loglikelihood, AIC, BIC). Rather, they become more relevant when we wish to compare the fit of two or more non-nested models. Given that, we will will ignore this section in this tutorial.
• Root mean square error of approximation (RMSEA). The root mean square error of approximation (RMSEA) is an absolute fit index that penalizes model complexity (e.g., models with a larger number of estimated parameters) and thus effectively rewards models that are more parsimonious. RMSEA values tend to upwardly biased when the model degrees of freedom are fewer (i.e., when the model is closer to being just-identified); further, Hu and Bentler (1999) noted that RMSEA may not be the best choice for smaller sample sizes (e.g., N \(<\) 250). In general, an RMSEA value that is less than or equal to .06 indicates good model fit to the data, although some relax that cutoff to .08 or even .10. For this model, RMSEA is .020, which indicates that the model fits the data acceptably.
• Standardized root mean square residual. Like the RMSEA, the standardized root mean square residual (SRMR) is an example of an absolute fit index. An SRMR value that is less than or equal to .06 generally indicates good fit to the data, although some relax that cutoff to .08. For this model, SRMR is equal to .024, which indicates that the model fits the data acceptably.

In sum, the chi-square (\(\chi^{2}\)) test, CFI, TLI, RMSEA, and SRMR model fit indices all indicate that our model fit the data acceptably based on conventional rules and thresholds. This level of agreement, however, is not always going to occur. For instance, it is relatively common for the \(\chi^{2}\) test to indicate a lack of acceptable fit while one or more of the relative or absolute fit indices indicates that fit is acceptable given the limitations of the \(\chi^{2}\) test. Further, there may be instances where only two or three out of five of these model fit indices indicate acceptable model fit. In such instances, we should not necessarily toss out the model entirely, but we should consider whether there are model misspecifications. Of course, if all five model indices are well beyond the conventional thresholds (in a bad way), then our model likely has major issues, and we should not proceed with interpreting the parameter estimates. Fortunately, for our model, all five model fit indices signal that the model fit the data acceptably, and thus we should feel confident proceeding forward with interpreting and evaluating the parameter estimates.

Evaluating parameter estimates. As noted above, our model showed acceptable fit to the data, so we can feel comfortable interpreting the parameter estimates. By default, the cfa function provides unstandardized parameter estimates, but if you recall, we also requested standardized parameter estimates. In the output, the unstandardized parameter estimates fall under the column titled Estimates, whereas the standardized factor loadings we’re interested in fall under the column titled Std.all.

• Factor loadings. The output section labeled Latent Variables contains our factor loadings. For this model, the loadings represent the effects of the latent factors for role clarity, task mastery, job satisfaction, and job performance on the their respective items. By default, the cfa function constrains the factor loading associated with the first indicator of each latent factor to 1 for model estimation purposes. Note, however, that there are still substantive standardized factor loadings for those first indicators, but they lack standard error (SE), z-value, and p-value estimates. We can still evaluate those standardized factor loadings, though. First, regarding the role clarity (RC) latent factor all standardized factor loadings (.682-.802) fell within Bagozzi and Yi’s (1988) recommended range of .50-.95. Second, regarding the task mastery (TM) latent factor, all standardized factor loadings (.753-.802) fell within recommended range of .50-.95. Third, regarding the job satisfaction (JS) latent factor, all standardized factor loadings (.734-.777) fell within recommended range of .50-.95. Fourth, regarding the job performance (JP) latent factor, all standardized factor loadings (.752-.801) fell within recommended range of .50-.95.
• Covariances. The output section labeled Covariances contains the pairwise covariance estimates for the four latent factors. As was the case with the factor loadings, we can view the standardized and unstandardized parameter estimates, where the standardized covariances can be interpreted as correlations. All six correlations are statistically significant (p < .05). In terms of practical significance, the correlations between RC and JS (.392), between TM and JS (.343), and between JS and JP (.386) are medium in magnitude. The correlations between RC and TM (.127), between RC and JP (.170), and between TM and JP (.162) are small in magnitude.
• Variances The output section labeled Variances contains the (residual error) variance estimates for each observed indicator (i.e., item) of the latent factor and for the latent factor itself. As was the case with the factor loadings, we can view the standardized and unstandardized parameter estimates.
  • Residual error variances for indicators. The estimates associated with the 16 indicator variables represent the residual error variances. Sometimes these are referred to as residual variances, disturbance terms, or uniquenesses. The standardized error variances ranged from .358 to .534, which can be interpreted as proportions of the variance not explained by the latent factor. For example, the latent factor RC failed to explain 53.4% of the variance in the indicator RC1, which is just outside the limit of what we conventionally consider to be acceptable; this suggests that 46.6% (100% - 53.4%) of the variance in indicator RC1 was explained by the latent factor RC. With the exception of the RC1 item’s error variance (.534), the indicator error variances were less than the recommended .50 threshold, which means that unmodeled constructs did not likely have a notable impact on the vast majority of the indicators. The standardized error variance for the RC1 item was just above the .50 recommended cutoff, and if we check the item’s content (“I understand what my job-related responsibilities are.”) and the construct’s conceptual definition (“the extent to which an individual understands what is expected of them in their job or role”), we see that the item fits within the conceptual definition boundaries; thus, we should retain the RC1 item.
  • Variance of the latent factors. The variance estimate for the latent factor provides can provide an indication of the latent factors’ level variability; however, its value depends on the scaling of factor loadings, and generally it is not a point of interest when evaluating CFA models. By default, the standardized variance for the latent factor will be equal to 1.000, and thus if we wished to evaluate the latent factor variance, we would interpret the unstandardized variance in this instance.

Within the semTools package, there are two additional diagnostic tools that we can apply to our model. Specifically, the AVE and compRelSEM functions allow us to estimate the average variance extracted (AVE) (Fornell and Larcker 1981) and the composite (construct) reliability (CR) (Bentler 1968). If you haven’t already, please install and access the semTools package.

# Install package
install.packages("semTools")

# Access package
library(semTools)

To estimate AVE, we simply specify the name of the AVE function, and within the function parentheses, we insert the name of our fitted CFA model estimate.

# Estimate average variance extracted (AVE)
AVE(cfa_fit)

##    RC    TM    JS    JP 
## 0.546 0.608 0.567 0.606

Average variance extracted (AVE). The AVE estimates were .546 (RC), .608 (TM), .567 (JS), and .606 (JP), which are above the conventional threshold (\(\ge\) .50). We can conclude that AVE estimates fare in the acceptable range.

# Estimate composite/construct reliability (CR)
compRelSEM(cfa_fit)

##    RC    TM    JS    JP 
## 0.827 0.861 0.840 0.860

Composite reliability (CR). The CR estimates were .827 (RC), .861 (TM), .840 (JS), and .860 (JP), which exceeded the conventional threshold for acceptable reliability (\(\ge\) .70) as well as the more relaxed “questionable” threshold (\(\ge\) .60). We can conclude that the four latent factors and associated indicators showed acceptably high reliability and specifically acceptably high internal consistency reliability.

Visualize the path diagram. To visualize our four-factor CFA measurement model as a path diagram, we can use the semPaths function from the semPlot package. If you haven’t already, please install and access the semPlot package.

# Install package
install.packages("semPlot")

# Access package
library(semPlot)

While there are many arguments that can be used to refine the path diagram visualization, we will focus on just four to illustrate how the semPaths function works.

1. As the first argument, insert the name of the fitted CFA model object (cfa_fit).
2. As the second argument, specify what="std" to display just the standardized parameter estimates.
3. As the third argument, specify weighted=FALSE to request that the visualization not weight the edges (e.g., lines) and other plot features.
4. As the fourth argument, specify nCharNodes=0 in order to use the full names of latent and observed indicator variables instead of abbreviating them.

# Visualize the measurement model
semPaths(cfa_fit,         # name of fitted model object 
         what="std",      # display standardized parameter estimates
         weighted=FALSE,  # do not weight plot features
         nCharNodes=0)    # do not abbreviate names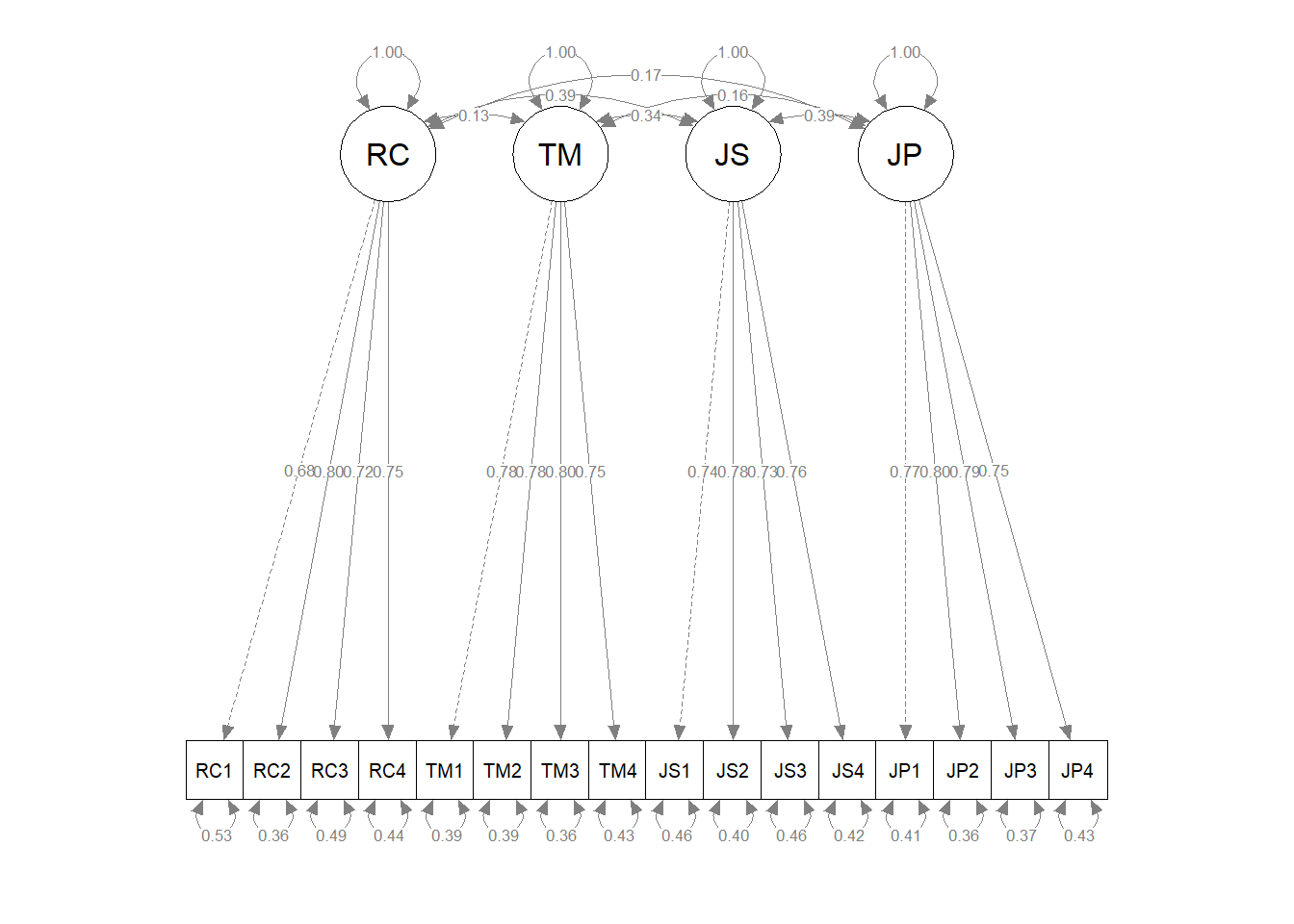

The resulting CFA path diagram can be useful for interpreting the model specifications and the parameter estimates.

In sum, the model fit indices suggested acceptable fit of the model to the data, and for the most part, the parameter estimates fell within acceptable ranges. The AVE and CR estimates also were acceptable. Given that our measurement model is acceptable, we are ready to specify and estimate a structural regression model by introducing direction paths (relations) into our model. Please note, however that we would typically take additional steps to compare different nested factor structures to evaluate whether a more parsimonious but equal-fitting measurement model exists. You can how to compare CFA nested model comparisons in a previous chapter.

58.2.5 Estimate a Structural Regression Model

In the previous section, we evaluated the measurement model of our four constructs (i.e., role clarity, task mastery, job satisfaction, job performance) by estimating a four-factor confirmatory factor analysis (CFA) model. In this section, we will add direction paths (relations) to the measurement model, which will result in a structural regression model (SRM). More specifically, we will specify an SRM that resembles Figure 3 that was presented earlier in the chapter; we will regress the job satisfaction (JS) latent factor onto the role clarity (RC) and task mastery (TM) latent factors, and we will regress the job performance (JP) latent factor onto the job satisfaction (JS) latent factor. Let’s assume that these model specifications are informed by extant theory.

To do so, we will use the sem function from the lavaan package. So, if you haven’t already, be sure that you have installed and accessed the lavaan package.

First, we will specify the SRM and assign it to an object that we can subsequently reference. To do so, we will do the following.

1. Specify a name for the model object (e.g., srm_mod), followed by the <- assignment operator.
2. To the right of the <- assignment operator and within quotation marks (" "):
3. Include the measurement model that we specified in the previous section.
4. Add direction paths (relations):

1. To specify the direct paths from RC to JS and from TM to JS, we will use the regression (~) operator. Specifically, we will specify JS followed by the ~ operator, the RC latent factor, the + operator, and the the TM latent factor, which looks like this: JS ~ RC + TM. In other words, we are regressing JS onto RC and TM.
2. To specify the direct path from JS to JP, we will use the regression (~) operator again. Specifically, we will specify JP followed by the ~ operator and then the JS latent factor, which looks like this: JP ~ JS. In other words, we are regressing JP onto JS.

# Specify four-factor SRM & assign to object
srm_mod <- "
# Measurement model
RC =~ RC1 + RC2 + RC3 + RC4
TM =~ TM1 + TM2 + TM3 + TM4
JS =~ JS1 + JS2 + JS3 + JS4
JP =~ JP1 + JP2 + JP3 + JP4

# Directional paths/relations
JS ~ RC + TM
JP ~ JS
"

Second, now that we have specified the model object (srm_mod), we are ready to estimate the model using the sem function from the lavaan package. To do so, we will do the following.

1. Specify a name for the fitted model object (e.g., srm_fit), followed by the <- assignment operator.
2. To the right of the <- assignment operator, type the name of the sem function, and within the function parentheses include the following arguments.

1. As the first argument, insert the name of the model object that we specified above (srm_mod).
2. As the second argument, insert the name of the data frame object to which the indicator (observed) variables in our model belong. That is, after data=, insert the name of the data frame object (df).

# Estimate four-factor SRM model & assign to fitted model object
srm_fit <- sem(srm_mod,      # name of specified model object
               data=df)      # name of data frame object

Third, we will use the summary function from base R to to print the model results. To do so, we will apply the following arguments in the summary function parentheses.

1. As the first argument, specify the name of the fitted model object that we created above (srm_fit).
2. As the second argument, set fit.measures=TRUE to obtain the model fit indices (e.g., CFI, TLI, RMSEA, SRMR).
3. As the third argument, set standardized=TRUE to request the standardized parameter estimates for the model.
4. As the fourth argument, set rsquare=TRUE to request the R² values for endogenous variables, i.e., outcome variables associated with each of the directional paths we specified; in this SRM, our substantive endogenous variables are JS and JP.

# Print summary of model results
summary(srm_fit,             # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE,   # request standardized estimates
        rsquare=TRUE)        # request R-squared estimates

## lavaan 0.6.15 ended normally after 31 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        36
## 
##   Number of observations                           550
## 
## Model Test User Model:
##                                                       
##   Test statistic                               120.858
##   Degrees of freedom                               100
##   P-value (Chi-square)                           0.076
## 
## Model Test Baseline Model:
## 
##   Test statistic                              3851.181
##   Degrees of freedom                               120
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.994
##   Tucker-Lewis Index (TLI)                       0.993
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -12612.020
##   Loglikelihood unrestricted model (H1)     -12551.591
##                                                       
##   Akaike (AIC)                               25296.040
##   Bayesian (BIC)                             25451.197
##   Sample-size adjusted Bayesian (SABIC)      25336.918
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.019
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.031
##   P-value H_0: RMSEA <= 0.050                    1.000
##   P-value H_0: RMSEA >= 0.080                    0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.025
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC =~                                                                 
##     RC1               1.000                               0.746    0.682
##     RC2               1.213    0.080   15.227    0.000    0.905    0.801
##     RC3               1.037    0.073   14.124    0.000    0.774    0.715
##     RC4               1.110    0.076   14.586    0.000    0.828    0.747
##   TM =~                                                                 
##     TM1               1.000                               0.923    0.783
##     TM2               1.051    0.058   18.232    0.000    0.970    0.783
##     TM3               0.998    0.054   18.643    0.000    0.921    0.801
##     TM4               0.985    0.056   17.520    0.000    0.909    0.753
##   JS =~                                                                 
##     JS1               1.000                               0.907    0.737
##     JS2               1.048    0.063   16.582    0.000    0.951    0.776
##     JS3               0.994    0.063   15.790    0.000    0.902    0.734
##     JS4               1.033    0.063   16.362    0.000    0.937    0.764
##   JP =~                                                                 
##     JP1               1.000                               1.168    0.766
##     JP2               1.102    0.061   18.192    0.000    1.288    0.801
##     JP3               0.981    0.054   18.044    0.000    1.146    0.794
##     JP4               0.994    0.058   17.122    0.000    1.161    0.752
## 
## Regressions:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   JS ~                                                                  
##     RC                0.433    0.063    6.871    0.000    0.356    0.356
##     TM                0.295    0.048    6.177    0.000    0.300    0.300
##   JP ~                                                                  
##     JS                0.501    0.067    7.529    0.000    0.389    0.389
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC ~~                                                                 
##     TM                0.087    0.035    2.478    0.013    0.127    0.127
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC1               0.639    0.047   13.654    0.000    0.639    0.535
##    .RC2               0.458    0.044   10.487    0.000    0.458    0.359
##    .RC3               0.571    0.044   13.026    0.000    0.571    0.488
##    .RC4               0.545    0.044   12.272    0.000    0.545    0.443
##    .TM1               0.538    0.044   12.283    0.000    0.538    0.387
##    .TM2               0.594    0.048   12.285    0.000    0.594    0.387
##    .TM3               0.472    0.040   11.699    0.000    0.472    0.358
##    .TM4               0.631    0.048   13.048    0.000    0.631    0.433
##    .JS1               0.693    0.053   13.005    0.000    0.693    0.457
##    .JS2               0.596    0.050   11.989    0.000    0.596    0.397
##    .JS3               0.696    0.053   13.064    0.000    0.696    0.461
##    .JS4               0.626    0.051   12.340    0.000    0.626    0.416
##    .JP1               0.960    0.075   12.723    0.000    0.960    0.413
##    .JP2               0.927    0.079   11.699    0.000    0.927    0.359
##    .JP3               0.771    0.065   11.939    0.000    0.771    0.370
##    .JP4               1.036    0.079   13.057    0.000    1.036    0.434
##     RC                0.556    0.066    8.372    0.000    1.000    1.000
##     TM                0.852    0.083   10.305    0.000    1.000    1.000
##    .JS                0.623    0.069    8.979    0.000    0.756    0.756
##    .JP                1.158    0.119    9.736    0.000    0.849    0.849
## 
## R-Square:
##                    Estimate
##     RC1               0.465
##     RC2               0.641
##     RC3               0.512
##     RC4               0.557
##     TM1               0.613
##     TM2               0.613
##     TM3               0.642
##     TM4               0.567
##     JS1               0.543
##     JS2               0.603
##     JS3               0.539
##     JS4               0.584
##     JP1               0.587
##     JP2               0.641
##     JP3               0.630
##     JP4               0.566
##     JS                0.244
##     JP                0.151

Evaluating model fit. Now that we have the summary of our model results, we will begin by evaluating key pieces of the model fit information provided in the output.

• Estimator. The function defaulted to using the maximum likelihood (ML) model estimator. When there are deviations from multivariate normality or categorical variables, the function may switch to another estimator; alternatively, we can manually switch to another estimator using the estimator= argument in the sem function.
• Number of parameters. Thirty-six parameters were estimated, which, as we will see later, correspond to the factor loadings, directional paths (i.e., regressions), covariances between exogenous latent factors (i.e., RC and TM), latent factor variances, and (residual) error term variances of the observed variables (i.e., indicators) and the endogenous latent factors (i.e., JS, JP).
• Number of observations. Our effective sample size is 550. Had there been missing data on the observed variables, this portion of the output would have indicated how many of the observations were retained for the analysis given the missing data. How missing data are handled during estimation will depend on the type of missing data approach we apply, which is covered in more default in the section called Estimating Models with Missing Data. By default, the sem function applies listwise deletion in the presence of missing data.
• Chi-square test. The chi-square (\(\chi^{2}\)) test assesses whether the model fits the data adequately, where a statistically significant \(\chi^{2}\) value (e.g., p \(<\) .05) indicates that the model does not fit the data well and a nonsignificant chi-square value (e.g., p \(\ge\) .05) indicates that the model fits the data reasonably well. The null hypothesis for the \(\chi^{2}\) test is that the model fits the data perfectly, and thus failing to reject the null model provides some confidence that the model fits the data reasonably close to perfectly. Of note, the \(\chi^{2}\) test is sensitive to sample size and non-normal variable distributions. For this model, we find the \(\chi^{2}\) test in the output section labeled Model Test User Model. Because the p-value is equal to or greater than .05, we fail to reject the null hypothesis that the mode fits the data perfectly and thus conclude that the model fits the data acceptably (\(\chi^{2}\) = 120.858, df = 100, p = .076). Finally, note that because the model’s degrees of freedom (i.e., 100) is greater than zero, we can conclude that the model is over-identified.
• Comparative fit index (CFI). As the name implies, the comparative fit index (CFI) is a type of comparative (or incremental) fit index, which means that CFI compares our estimated model to a baseline model, which is commonly referred to as the null or independence model. CFI is generally less sensitive to sample size than the chi-square (\(\chi^{2}\)) test. A CFI value greater than or equal to .95 generally indicates good model fit to the data, although some might relax that cutoff to .90. For this model, CFI is equal to .994, which indicates that the model fits the data acceptably.
• Tucker-Lewis index (TLI). Like CFI, Tucker-Lewis index (TLI) is another type of comparative (or incremental) fit index. TLI is generally less sensitive to sample size than the chi-square test and tends to work well with smaller sample sizes; however, TLI may be not be the best choice for smaller sample sizes (e.g., N \(<\) 250). A TLI value greater than or equal to .95 generally indicates good model fit to the data, although like CFI, some might relax that cutoff to .90. For this model, TLI is equal to .993, which indicates that the model fits the data acceptably.
• Loglikelihood and Information Criteria. The section labeled Loglikelihood and Information Criteria contains model fit indices that are not directly interpretable on their own (e.g., loglikelihood, AIC, BIC). Rather, they become more relevant when we wish to compare the fit of two or more non-nested models. Given that, we will will ignore this section in this tutorial.
• Root mean square error of approximation (RMSEA). The root mean square error of approximation (RMSEA) is an absolute fit index that penalizes model complexity (e.g., models with a larger number of estimated parameters) and thus effectively rewards models that are more parsimonious. RMSEA values tend to upwardly biased when the model degrees of freedom are fewer (i.e., when the model is closer to being just-identified); further, RMSEA may not be the best choice for smaller sample sizes (e.g., N \(<\) 250). In general, an RMSEA value that is less than or equal to .06 indicates good model fit to the data, although some relax that cutoff to .08 or even .10. For this model, RMSEA is .019, which indicates that the model fits the data acceptably.
• Standardized root mean square residual. Like the RMSEA, the standardized root mean square residual (SRMR) is an example of an absolute fit index. An SRMR value that is less than or equal to .06 generally indicates good fit to the data, although some relax that cutoff to .08. For this model, SRMR is equal to .025, which indicates that the model fits the data acceptably.

In sum, the chi-square (\(\chi^{2}\)) test, CFI, TLI, RMSEA, and SRMR model fit indices all indicate that our model fit the data acceptably based on conventional rules of thumb and thresholds. This level of agreement, however, is not always going to occur. For instance, it is relatively common for the \(\chi^{2}\) test to indicate a lack of acceptable fit while one or more of the relative or absolute fit indices indicates that fit is acceptable given the limitations of the \(\chi^{2}\) test. Further, there may be instances where only two or three out of five of these model fit indices indicate acceptable model fit. In such instances, we should not necessarily toss out the model entirely, but we should consider whether there are model misspecifications. Of course, if all five model indices are well beyond the conventional thresholds (in a bad way), then our model may have some major misspecification issues, and we should proceed thoughtfully when interpreting the parameter estimates.

Evaluating parameter estimates. As noted above, our model showed acceptable fit to the data, so we can feel comfortable interpreting the parameter estimates. By default, the sem function provides unstandardized parameter estimates, but if you recall, we also requested standardized parameter estimates. In the output, the unstandardized parameter estimates fall under the column titled Estimates, whereas the standardized factor loadings we’re interested in fall under the column titled Std.all. Assuming we have already evaluated the measurement structure using a CFA model, with an SRM, we are often most interested in reviewing the directional paths (relations) and covariances involving the latent factors, so we’ll begin with those parameter estimates.

• Directional paths (relations). The output section labeled Regressions contains the directional path (relation) estimates that we specified. We can view the standardized and unstandardized parameter estimates, where the unstandardized estimates can be interpreted as unstandardized regression coefficients and the standardized estimates can be interpreted as standardized regression coefficients. First, the standardized directional path from RC to JS is statistically significant and positive, indicating that those with higher RC tend to have higher JS (.356, p < .001). Second, the standardized directional path from TM to JS is statistically significant and positive, indicating that those with higher TM tend to have higher JS (.300, p < .001). Third, the standardized directional path from JS to JP is statistically significant and positive, indicating that those with higher JS tend to have higher JP (.389, p < .001).
• Covariances. The output section labeled Covariances contains the covariance estimate for the two exogenous latent factors, which are those latent factors that do not serve as an outcome (i.e., JS, JP). As was the case with the directional paths, we can view the standardized and unstandardized parameter estimate, where the standardized covariance can be interpreted as a correlation. The correlation between JS and JP (.127) is statistically significant (p = .013), positive, and small in terms of practical significance.
• Factor loadings. The output section labeled Latent Variables contains our factor loadings. For this model, the loadings represent the effects of the latent factors for role clarity, task mastery, job satisfaction, and job performance on the their respective items. By default, the sem function constrains the factor loading associated with the first indicator of each latent factor to 1 for model estimation purposes. Note, however, that there are still substantive standardized factor loadings for those first indicators, but they lack standard error (SE), z-value, and p-value estimates. We can still evaluate those standardized factor loadings, though. First, regarding the role clarity (RC) latent factor all standardized factor loadings (.682-.801) fell within Bagozzi and Yi’s (1988) recommended range of .50-.95. Second, regarding the task mastery (TM) latent factor, all standardized factor loadings (.753-.801) fell within recommended range of .50-.95. Third, regarding the job satisfaction (JS) latent factor, all standardized factor loadings (.734-.776) fell within recommended range of .50-.95. Fourth, regarding the job performance (JP) latent factor, all standardized factor loadings (.752-.801) fell within recommended range of .50-.95.
• Variances The output section labeled Variances contains the (residual error) variance estimates for each observed indicator (i.e., item) of the latent factor and for the latent factor itself. As was the case with the factor loadings, we can view the standardized and unstandardized parameter estimates.
  • (Residual error) variances for indicators. The estimates associated with the 16 indicator variables represent the residual error variances. Sometimes these are referred to as residual variances, disturbance terms, or uniquenesses. The standardized error variances ranged from .359 to .535, which can be interpreted as proportions of the variance not explained by the latent factor. For example, the latent factor RC failed to explain 53.5% of the variance in the indicator RC1, which is just outside the limit of what we conventionally consider to be acceptable; this suggests that 46.5% (100% - 53.5%) of the variance in indicator RC1 was explained by the latent factor RC. With the exception of the RC1 item’s error variance (.535), the indicator error variances were less than the recommended .50 threshold, which means that unmodeled constructs did not likely have a notable impact on the vast majority of the indicators. The standardized error variance for the RC1 item was just above the .50 recommended cutoff, and if we check the item’s content (“I understand what my job-related responsibilities are.”) and the construct’s conceptual definition (“the extent to which an individual understands what is expected of them in their job or role”), we see that the item fits within the conceptual definition boundaries; thus, we should retain the RC1 item.
  • Variance of the latent factors. The variance estimate for the latent factor provides can provide an indication of the latent factors’ level variability; however, its value depends on the scaling of factor loadings, and generally it is not a point of interest when evaluating CFA models. By default, the standardized variance for the latent factor will be equal to 1.000, and thus if we wished to evaluate the latent factor variance, we would interpret the unstandardized variance in this instance.
  • R-squared. For all endogenous variables (i.e., those variables that serve as an outcome variable of some kind), an R² estimate is provided. The R² estimates associated with the indicator variables are equal to 1 minus the standardized (residual error) variance (see above), and thus they do not provide additional information. The R² estimates associated with the endogenous latent factors, however, are of substantive interest. Specifically, for JS, R² equaled .244, which indicates that collectively RC and TM explained 24.4% of the variance in JS, which is a small or small/medium effect. For JP, R² equaled .151, which indicates that JS explained 15.1% of the variance in JP, which is a small effect.

Visualize the path diagram. To visualize our unconditional unconstrained LGM as a path diagram, we can use the semPaths function from the semPlot package. If you haven’t already, please install and access the semPlot package. While there are many arguments that can be used to refine the path diagram visualization, we will focus on just four to illustrate how the semPaths function works.

1. As the first argument, insert the name of the fitted LGM object (lgm_fit).
2. As the second argument, specify what="est" to display just the unstandardized parameter estimates.
3. As the third argument, specify weighted=FALSE to request that the visualization not weight the edges (e.g., lines) and other plot features.
4. As the fourth argument, specify nCharNodes=0 in order to use the full names of latent and observed indicator variables instead of abbreviating them.

# Visualize the four-factor SRM
semPaths(srm_fit,         # name of fitted model object 
         what="std",      # display standardized parameter estimates
         weighted=FALSE,  # do not weight plot features
         nCharNodes=0)    # do not abbreviate names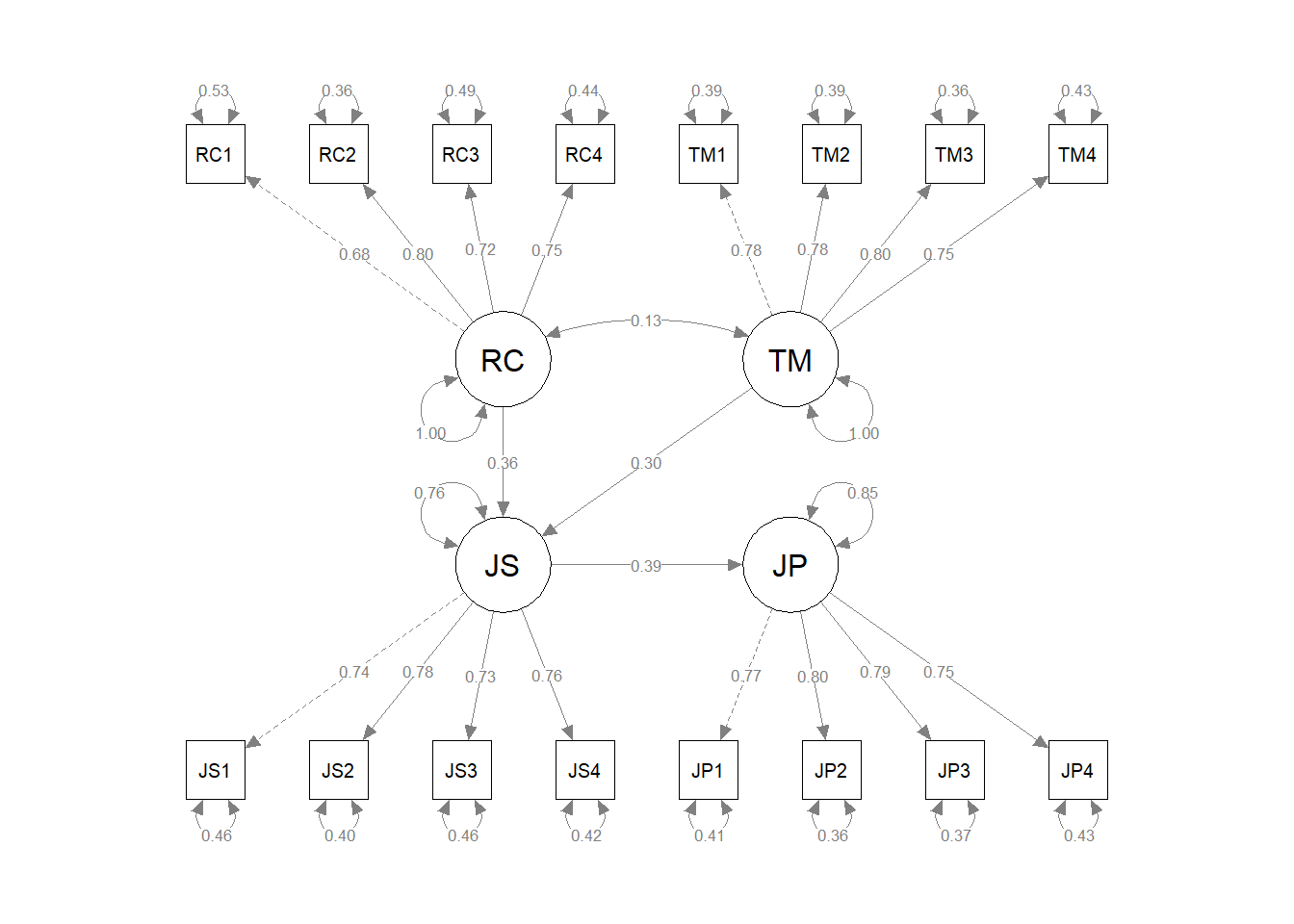

The resulting path diagram can be useful for interpreting the model specifications and the parameter estimates.

Results write-up for the SRM. After their respective start dates, we assessed 550 new employees’ role clarity (1 month post-hire), task mastery (1 month post-hire), job satisfaction (6 months post-hire), and supervisor-rated job satisfaction (6 months post-hire); missing data were not a concern. Each construct’s associated multi-item measure included four items. We hypothesized that higher role clarity and task mastery is associated with higher job satisfaction, and that higher job satisfaction is associated with higher job performance. Before estimating a structural regression model to test those hypotheses, we evaluated the measurement structure of the four measures using a multi-factor confirmatory factor analysis model. We evaluated the model’s fit to the data using the chi-square (\(\chi^{2}\)) test, CFI, TLI, RMSEA, and SRMR model fit indices. The \(\chi^{2}\) test indicated that the model fit the data as well as a perfectly fitting model (\(\chi^{2}\) = 120.274 df = 98, p = .063). Further, the CFI and TLI estimates were .994 and .993, respectively, which exceeded the more stringent threshold of .95, thereby indicating that model showed acceptable fit to the data. Similarly, the RMSEA estimate was .020, which was below the more stringent threshold of .06, thereby indicating that model showed acceptable fit to the data. The SRMR estimate was .024, which was below the stringent threshold of .06, thereby indicating acceptable model fit to the data. Collectively, the model fit information indicated that the four-factor measurement model fit the data acceptably. Further, standardized factor loadings ranged from .682 to .802, which all fell well within the recommended .50-.95 acceptability range. The standardized error variances for items ranged from .358 to .534, and only one estimate associated with the first role clarity item was above the the target threshold of .50, thereby indicating that it was unlikely that an unmodeled construct had an outsized influence on the items. The average variance extracted (AVE) estimates for role clarity, task mastery, job satisfaction, and job performance were .546, .608, .567, and .606, respectively, which all exceeded the .50 cutoff; thus, all four latent factors showed acceptable AVE levels. The composite reliability (CR) estimates for role clarity, task mastery, job satisfaction, and job performance were were .827, .861, .840, and .860, and all indicated acceptable levels of internal consistency reliability. In sum, the updated four-factor measurement model also showed acceptable fit to the data and acceptable parameter estimates, acceptable AVE estimates, and acceptable CR estimates; thus using the four-factor measurement model, we proceeded with estimating a structural regression model to test our hypotheses. The \(\chi^{2}\) test indicated that the model fit the data as well as a perfectly fitting model (\(\chi^{2}\) = 120.858 df = 100, p = .076). Further, the CFI and TLI estimates were .994 and .993, respectively, which exceeded the more stringent threshold of .95, thereby indicating that model showed acceptable fit to the data. Similarly, the RMSEA estimate was .019, which was below the more stringent threshold of .06, thereby indicating that model showed acceptable fit to the data. The SRMR estimate was .025, which was below the stringent threshold of .06, thereby indicating acceptable model fit to the data. Collectively, the model fit information indicated that the SRM fit the data acceptably. As hypothesized, the standardized directional path from: (a) role clarity to job satisfaction was statistically significant and positive (.356, p < .001); (b) from task mastery to job satisfaction was statistically significant and positive (.300, p < .001); and (c) from job satisfaction to job performance was statistically significant and positive (.389, p < .001).

58.2.6 Nested Model Comparisons

When possible, we typically prefer to arrive at a model that not only fits the data but also is parsimonious in nature (i.e., less complex). In some situations, we may wish to evaluate a more complex model that contains additional directional paths (relations) beyond what we hypothesized. For instance, in the SRM we estimated in the previous section, we treated the JS latent factor as an implied mediator, such that RC and TM predicted JS and JS predicted JP; in that model, we did not specify directional paths from RC and TM to JP, presumably because that was not consistent with theory. By omitting those directional paths, we implicitly constrained those paths to zero when estimating the model. When a predictor variable is only specified as a predictor of the mediator and not the outcome variable, this is referred to as a full mediation model (or complete mediation model). In contrast, a partial mediation model includes directional paths from the predictor to the outcome variable. Given that distinction, let’s compare the full mediation SRM from the previous section to a partial mediation SRM, where the full mediation SRM is nested within the partial mediation SRM. If the full mediation SRM’s fit to the data is no worse than than the partial mediation SRM’s fit to the data, then we should go with the the more parsimonious model (i.e., fewer freely estimated parameters). For a review of partial versus full mediation, please check out the earlier chapter on mediation using path analysis.

58.2.6.1 Estimate Full Mediation Model

We will begin by re-estimating our SRM from the previous section, which (as explained above) is an example of a full mediation model. The reason for re-estimating the model is to rename the specified model object and fitted model object to reflect the full mediation.

# Specify full mediation SRM & assign to object
srm_mod_full <- "
# Measurement model
RC =~ RC1 + RC2 + RC3 + RC4
TM =~ TM1 + TM2 + TM3 + TM4
JS =~ JS1 + JS2 + JS3 + JS4
JP =~ JP1 + JP2 + JP3 + JP4

# Directional paths/relations
JS ~ RC + TM
JP ~ JS
"

# Estimate full mediation SRM model & assign to fitted model object
srm_fit_full <- sem(srm_mod_full,     # name of specified model object
                    data=df)          # name of data frame object

# Print summary of model results
summary(srm_fit_full,        # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE,   # request standardized estimates
        rsquare=TRUE)        # request R-squared estimates

## lavaan 0.6.15 ended normally after 31 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        36
## 
##   Number of observations                           550
## 
## Model Test User Model:
##                                                       
##   Test statistic                               120.858
##   Degrees of freedom                               100
##   P-value (Chi-square)                           0.076
## 
## Model Test Baseline Model:
## 
##   Test statistic                              3851.181
##   Degrees of freedom                               120
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.994
##   Tucker-Lewis Index (TLI)                       0.993
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -12612.020
##   Loglikelihood unrestricted model (H1)     -12551.591
##                                                       
##   Akaike (AIC)                               25296.040
##   Bayesian (BIC)                             25451.197
##   Sample-size adjusted Bayesian (SABIC)      25336.918
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.019
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.031
##   P-value H_0: RMSEA <= 0.050                    1.000
##   P-value H_0: RMSEA >= 0.080                    0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.025
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC =~                                                                 
##     RC1               1.000                               0.746    0.682
##     RC2               1.213    0.080   15.227    0.000    0.905    0.801
##     RC3               1.037    0.073   14.124    0.000    0.774    0.715
##     RC4               1.110    0.076   14.586    0.000    0.828    0.747
##   TM =~                                                                 
##     TM1               1.000                               0.923    0.783
##     TM2               1.051    0.058   18.232    0.000    0.970    0.783
##     TM3               0.998    0.054   18.643    0.000    0.921    0.801
##     TM4               0.985    0.056   17.520    0.000    0.909    0.753
##   JS =~                                                                 
##     JS1               1.000                               0.907    0.737
##     JS2               1.048    0.063   16.582    0.000    0.951    0.776
##     JS3               0.994    0.063   15.790    0.000    0.902    0.734
##     JS4               1.033    0.063   16.362    0.000    0.937    0.764
##   JP =~                                                                 
##     JP1               1.000                               1.168    0.766
##     JP2               1.102    0.061   18.192    0.000    1.288    0.801
##     JP3               0.981    0.054   18.044    0.000    1.146    0.794
##     JP4               0.994    0.058   17.122    0.000    1.161    0.752
## 
## Regressions:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   JS ~                                                                  
##     RC                0.433    0.063    6.871    0.000    0.356    0.356
##     TM                0.295    0.048    6.177    0.000    0.300    0.300
##   JP ~                                                                  
##     JS                0.501    0.067    7.529    0.000    0.389    0.389
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC ~~                                                                 
##     TM                0.087    0.035    2.478    0.013    0.127    0.127
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC1               0.639    0.047   13.654    0.000    0.639    0.535
##    .RC2               0.458    0.044   10.487    0.000    0.458    0.359
##    .RC3               0.571    0.044   13.026    0.000    0.571    0.488
##    .RC4               0.545    0.044   12.272    0.000    0.545    0.443
##    .TM1               0.538    0.044   12.283    0.000    0.538    0.387
##    .TM2               0.594    0.048   12.285    0.000    0.594    0.387
##    .TM3               0.472    0.040   11.699    0.000    0.472    0.358
##    .TM4               0.631    0.048   13.048    0.000    0.631    0.433
##    .JS1               0.693    0.053   13.005    0.000    0.693    0.457
##    .JS2               0.596    0.050   11.989    0.000    0.596    0.397
##    .JS3               0.696    0.053   13.064    0.000    0.696    0.461
##    .JS4               0.626    0.051   12.340    0.000    0.626    0.416
##    .JP1               0.960    0.075   12.723    0.000    0.960    0.413
##    .JP2               0.927    0.079   11.699    0.000    0.927    0.359
##    .JP3               0.771    0.065   11.939    0.000    0.771    0.370
##    .JP4               1.036    0.079   13.057    0.000    1.036    0.434
##     RC                0.556    0.066    8.372    0.000    1.000    1.000
##     TM                0.852    0.083   10.305    0.000    1.000    1.000
##    .JS                0.623    0.069    8.979    0.000    0.756    0.756
##    .JP                1.158    0.119    9.736    0.000    0.849    0.849
## 
## R-Square:
##                    Estimate
##     RC1               0.465
##     RC2               0.641
##     RC3               0.512
##     RC4               0.557
##     TM1               0.613
##     TM2               0.613
##     TM3               0.642
##     TM4               0.567
##     JS1               0.543
##     JS2               0.603
##     JS3               0.539
##     JS4               0.584
##     JP1               0.587
##     JP2               0.641
##     JP3               0.630
##     JP4               0.566
##     JS                0.244
##     JP                0.151

# Visualize the full mediation SRM
semPaths(srm_fit_full,    # name of fitted model object 
         what="std",      # display standardized parameter estimates
         weighted=FALSE,  # do not weight plot features
         nCharNodes=0)    # do not abbreviate names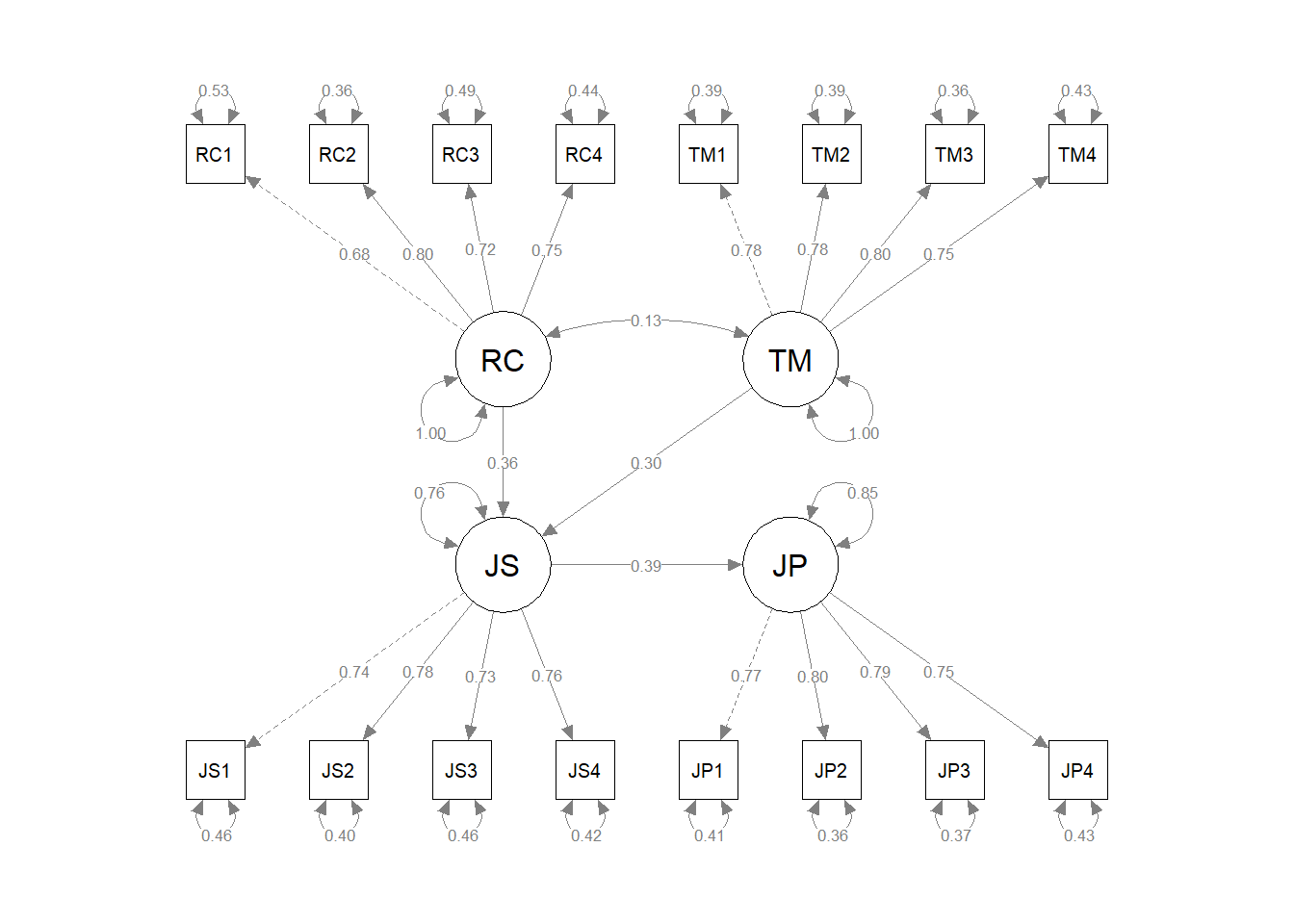

To save space, I summarize the full mediation model’s fit indices in the table below.

Model	\(\chi^{2}\)	df	p	CFI	TLI	RMSEA	SRMR
Full Mediation Model	120.858	100	.076	.994	.993	.019	.025

As reviewed in the previous section, this model fit the data acceptably. The directional paths from RC and TM to JS and from JS to JP were statistically significant and positive. Because this was a full mediation model, the directional paths from RC and TM to JP were not reported, as by default, they were constrained to zero.

58.2.6.2 Estimate Partial Mediation Model

We will treat the full mediation model from the previous section as our nested model, and in this section, we will compare the full mediation model to the more complex full partial mediation model (i.e., more freely estimated parameters). Specifically, we will specify a model in which we freely estimate the directional paths from RC and TM to JP. We’ll begin with the same model specifications as the full mediation model but add the additional regressions associated with those two directional paths.

# Specify partial mediation SRM & assign to object
srm_mod_partial <- "
# Measurement model
RC =~ RC1 + RC2 + RC3 + RC4
TM =~ TM1 + TM2 + TM3 + TM4
JS =~ JS1 + JS2 + JS3 + JS4
JP =~ JP1 + JP2 + JP3 + JP4

# Directional paths/relations
JS ~ RC + TM
JP ~ JS
JP ~ RC + TM # Added directional paths
"

# Estimate partial mediation SRM model & assign to fitted model object
srm_fit_partial <- sem(srm_mod_partial, # name of specified model object
                       data=df)         # name of data frame object

# Print summary of model results
summary(srm_fit_partial,     # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE,   # request standardized estimates
        rsquare=TRUE)        # request R-squared estimates

## lavaan 0.6.15 ended normally after 34 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        38
## 
##   Number of observations                           550
## 
## Model Test User Model:
##                                                       
##   Test statistic                               120.274
##   Degrees of freedom                                98
##   P-value (Chi-square)                           0.063
## 
## Model Test Baseline Model:
## 
##   Test statistic                              3851.181
##   Degrees of freedom                               120
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.994
##   Tucker-Lewis Index (TLI)                       0.993
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -12611.728
##   Loglikelihood unrestricted model (H1)     -12551.591
##                                                       
##   Akaike (AIC)                               25299.456
##   Bayesian (BIC)                             25463.233
##   Sample-size adjusted Bayesian (SABIC)      25342.605
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.020
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.032
##   P-value H_0: RMSEA <= 0.050                    1.000
##   P-value H_0: RMSEA >= 0.080                    0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.024
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC =~                                                                 
##     RC1               1.000                               0.746    0.682
##     RC2               1.213    0.080   15.227    0.000    0.905    0.801
##     RC3               1.038    0.073   14.127    0.000    0.774    0.716
##     RC4               1.110    0.076   14.587    0.000    0.828    0.747
##   TM =~                                                                 
##     TM1               1.000                               0.923    0.783
##     TM2               1.051    0.058   18.231    0.000    0.970    0.783
##     TM3               0.998    0.054   18.646    0.000    0.921    0.802
##     TM4               0.985    0.056   17.521    0.000    0.909    0.753
##   JS =~                                                                 
##     JS1               1.000                               0.908    0.737
##     JS2               1.048    0.063   16.585    0.000    0.951    0.777
##     JS3               0.994    0.063   15.793    0.000    0.902    0.734
##     JS4               1.033    0.063   16.368    0.000    0.937    0.764
##   JP =~                                                                 
##     JP1               1.000                               1.168    0.766
##     JP2               1.103    0.061   18.202    0.000    1.289    0.801
##     JP3               0.980    0.054   18.031    0.000    1.145    0.793
##     JP4               0.994    0.058   17.123    0.000    1.161    0.752
## 
## Regressions:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   JS ~                                                                  
##     RC                0.431    0.063    6.837    0.000    0.355    0.355
##     TM                0.293    0.048    6.123    0.000    0.298    0.298
##   JP ~                                                                  
##     JS                0.471    0.078    6.070    0.000    0.366    0.366
##     RC                0.034    0.083    0.412    0.680    0.022    0.022
##     TM                0.042    0.064    0.660    0.509    0.034    0.034
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC ~~                                                                 
##     TM                0.087    0.035    2.478    0.013    0.127    0.127
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC1               0.639    0.047   13.652    0.000    0.639    0.534
##    .RC2               0.458    0.044   10.494    0.000    0.458    0.359
##    .RC3               0.571    0.044   13.023    0.000    0.571    0.488
##    .RC4               0.545    0.044   12.272    0.000    0.545    0.443
##    .TM1               0.538    0.044   12.283    0.000    0.538    0.387
##    .TM2               0.594    0.048   12.289    0.000    0.594    0.387
##    .TM3               0.472    0.040   11.698    0.000    0.472    0.358
##    .TM4               0.631    0.048   13.049    0.000    0.631    0.433
##    .JS1               0.692    0.053   12.988    0.000    0.692    0.457
##    .JS2               0.596    0.050   11.972    0.000    0.596    0.397
##    .JS3               0.696    0.053   13.053    0.000    0.696    0.461
##    .JS4               0.625    0.051   12.321    0.000    0.625    0.416
##    .JP1               0.961    0.075   12.727    0.000    0.961    0.413
##    .JP2               0.925    0.079   11.682    0.000    0.925    0.358
##    .JP3               0.773    0.065   11.957    0.000    0.773    0.371
##    .JP4               1.035    0.079   13.056    0.000    1.035    0.434
##     RC                0.557    0.066    8.373    0.000    1.000    1.000
##     TM                0.852    0.083   10.305    0.000    1.000    1.000
##    .JS                0.625    0.070    8.979    0.000    0.759    0.759
##    .JP                1.159    0.119    9.744    0.000    0.850    0.850
## 
## R-Square:
##                    Estimate
##     RC1               0.466
##     RC2               0.641
##     RC3               0.512
##     RC4               0.557
##     TM1               0.613
##     TM2               0.613
##     TM3               0.642
##     TM4               0.567
##     JS1               0.543
##     JS2               0.603
##     JS3               0.539
##     JS4               0.584
##     JP1               0.587
##     JP2               0.642
##     JP3               0.629
##     JP4               0.566
##     JS                0.241
##     JP                0.150

# Visualize the partial mediation SRM
semPaths(srm_fit_partial, # name of fitted model object 
         what="std",      # display standardized parameter estimates
         weighted=FALSE,  # do not weight plot features
         nCharNodes=0)    # do not abbreviate names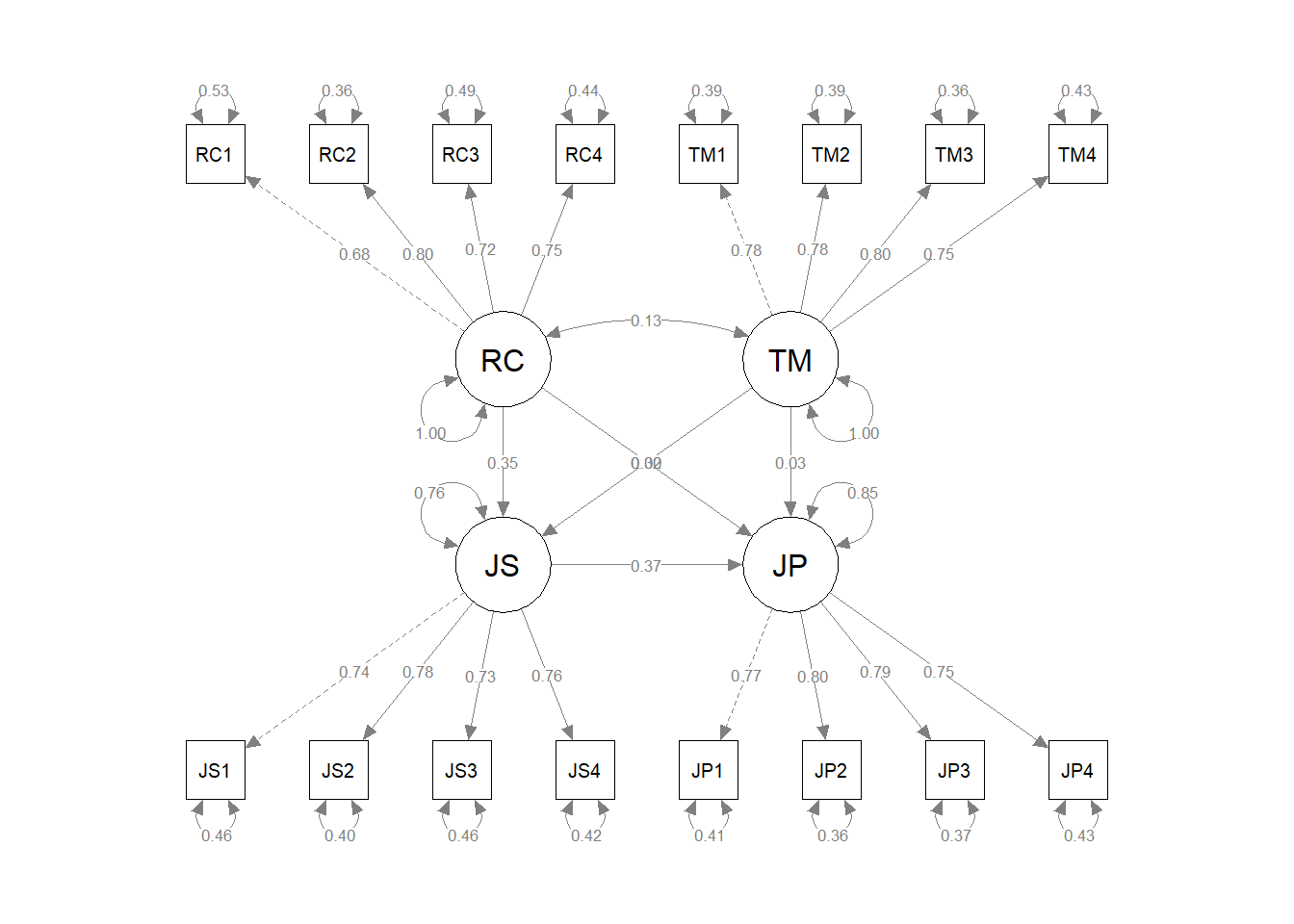

Below, I’ve expanded upon the previous table by adding in the model fit information for the partial mediation model.

Model	\(\chi^{2}\)	df	p	CFI	TLI	RMSEA	SRMR
Full Mediation Model	120.858	100	.076	.994	.993	.019	.025
Partial Mediation Model	120.274	98	.063	.994	.993	.020	.024

Like the full mediation model, the partial mediation model fit the data acceptably. The directional paths from RC and TM to JS and from JS to JP remained statistically significant and positive, and the new directional paths from RC and TM to JP were not statistically significant.

As an additional test, we can perform a nested model comparison using the chi-square (\(\chi^{2}\)) difference test, which is also known as the log-likelihood (LL) test. To perform this test, we’ll apply the anova function from base R. As the first argument, we’ll insert the name of our fitted partial mediation model object (srm_fit_partial), and as the second argument, we’ll insert the name of our full mediation model object (srm_fit_full).

# Nested model comparison using chi-square difference test
anova(srm_fit_partial, srm_fit_full)

## 
## Chi-Squared Difference Test
## 
##                  Df   AIC   BIC  Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
## srm_fit_partial  98 25300 25463 120.27                                    
## srm_fit_full    100 25296 25451 120.86    0.58421     0       2     0.7467

The chi-square difference test indicates that the partial mediation model and full mediation model fit the data approximately the same (\(\Delta \chi^{2}\) = .58421, \(\Delta df\) = 2, \(p\) = .7467). Given that full mediation model is more parsimonious and is presumably consistent with theory, we will retain the full mediation model.

Note: If your anova function output defaulted to scientific notation, you can “turn off” scientific notation using the following function. After running the options function below, you can re-run the anova function to get the output in traditional notation.

# Turn off scientific notation
options(scipen=9999)

58.2.6.3 Create a Matrix Comparing Model Fit Indices

If our goals are to create a matrix containing only those model fit indices that we covered in this chapter and to add in the chi-square difference tests, we can do the following, which incorporates the inspect function from the lavaan package and the cbind, rbind, and t functions from base R.

# Create object containing selected fit indices
select_fit_indices <- c("chisq","df","pvalue","cfi","tli","rmsea","srmr")

# Create matrix comparing model fit indices
compare_mods <- cbind(
  inspect(srm_fit_partial, "fit.indices")[select_fit_indices],
  inspect(srm_fit_full, "fit.indices")[select_fit_indices]
  )

# Add more informative model names to matrix columns
colnames(compare_mods) <- c("Partial Mediation Model", 
                            "Full Mediation Model")

# Create vector of chi-square difference tests (nested model comparisons)
`chisq diff (p-value)` <- c(NA,
                            anova(srm_fit_full, 
                                  srm_fit_partial)$`Pr(>Chisq)`[2])

# Add chi-square difference tests to matrix object
compare_mods <- rbind(compare_mods, `chisq diff (p-value)`)

# Round object values to 3 places after decimal
compare_mods <- round(compare_mods, 3)

# Rotate matrix
compare_mods <- t(compare_mods)

# Print object
print(compare_mods)

##                           chisq  df pvalue   cfi   tli rmsea  srmr chisq diff (p-value)
## Partial Mediation Model 120.274  98  0.063 0.994 0.993 0.020 0.024                   NA
## Full Mediation Model    120.858 100  0.076 0.994 0.993 0.019 0.025                0.747

58.2.7 Estimating Indirect Effects in Mediation Models

As noted in the previous section, our focal model in this chapter is a mediation model, as the JS latent factor mediates the associations between the RC and TM latent factors and the JP latent factor. To this point, however, we have not yet evaluated whether there is evidence of statistically significant indirect effects, such that the effects of RC and TM on JP are transmitted via JS. Thus, in this section, we will learn how to estimate indirect effects for a mediation model using a structural regression model (SRM). Mediation and indirect effects were covered in a previous chapter involving path analysis with observed variables only, and in this chapter, we will expand upon that framework. If you haven’t already, I recommend checking out that previous chapter on mediation using path analysis, as in that chapter I provide a more in-depth explanation of different approaches to estimating indirect effects.

As covered in the earlier chapter on mediation using path analysis, the percentile bootstrapping method is generally recommended over the delta method, and thus, my recommendation is to use the percentile bootstrapping method when estimating indirect effects. Depending upon the processing speed and power of your machine, the approach make take a minute or multiple minutes to perform the number of bootstrap iterations (i.e., re-samples) requested. We will adapt the model specification syntax from the previous section, where we learned how to estimate a full mediation model (given that it is more parsimonious than the partial mediation model yet fit no worse).

1. To begin, if you haven’t already, install and access the lavaan package, as well will be using the sem and parameterEstimates functions from that package.
2. We’ll adapt the model specifications from the full mediation model (see earlier section), and name the model specification object something (e.g., srm_mod_full).

1. The measurement model syntax will remain the same.
2. For the directional paths (relations) from the predictor variable(s) to the mediator variable(s), we will precede each predictor variable (to the right of the ~ operator) with a letter or word that we can subsequently use to extract the estimated coefficient. Conventionally, we name the paths from the predictor variable(s) to the mediator variable(s) a. Because we have more than one of these paths, let’s name the path associated with RC in relation to JS with a1, and for the path associated with TM in relation to JS, let’s name it a2.
3. For the directional paths (relations) from the mediator variable(s) to the outcome variable(s), we will precede each mediator variable (to the right of the ~ operator) with a letter or word that we can subsequently use to extract the estimated coefficient. Conventionally, we name the paths from the mediator variable(s) to the outcome variable(s) b. Because we have just one of these paths, let’s name the path associated with JS in relation to JP with b.
4. To estimate the indirect effects, we need to multiply each a path with each b path. Working from left to right, let’s name the indirect effect involving the a1 and b paths a1b. To the right of a1b, insert the := operator. To the right of the := operator, multiply the a1 path coefficient by the b path coefficient, which should look like: a1b := a1*b. Repeat the same process for the a2 and b paths, which should look like: a2b := a2*b.

# Specify full mediation SRM & assign to object
srm_mod_full <- "
# Measurement model
RC =~ RC1 + RC2 + RC3 + RC4
TM =~ TM1 + TM2 + TM3 + TM4
JS =~ JS1 + JS2 + JS3 + JS4
JP =~ JP1 + JP2 + JP3 + JP4

# Directional paths/relations
JS ~ a1*RC + a2*TM
JP ~ b*JS

# Indirect effects (a*b)
a1b := a1*b
a2b := a2*b
"

Because we’ve specified our model and indirect effects, we are ready to estimate the model using the sem function.

1. To make our bootrapping reproducible, set a seed using the set.seed function and a number of your choosing within the function parentheses.
2. As we did in the previous section, name the fitted model object srm_fit_full using the assignment <- operator.
3. Estimate the model using the sem function.

1. As the first argument, insert the name of the specified model object (srm_mod_full).
2. As the second argument, specify data= followed by the name of the data frame object to which the variables in the model belong (df).
3. As the third argument, specify the approach for estimating the standard errors by typing se= followed by bootstrap. Doing so will request bootstrap standard errors.
4. As the fourth argument, type bootstrap= followed by the number of bootstrap re-samples (with replacement) we wish to request. Generally, requesting at least 5,000 re-sampling iterations is advisable, so let’s specify the following: bootstrap=5000. Depending on your computer, the bootstrapping estimation could take a a minute or two to complete.

# Set seed
set.seed(2024)

# Estimate full mediation SRM model & assign to fitted model object
srm_fit_full <- sem(srm_mod_full,     # name of specified model object
                    data=df,          # name of data frame object
                    se="bootstrap",   # request bootstrapped standard errors
                    bootstrap=5000)   # request 5,000 bootstrap re-samples

To evaluate the model fit indices and direct effects, we will apply the summary function from base R in the same manner as we have thus far in the chapter. That is, as the first argument, type the name of the model specification object we created (srm_fit_full). As the second and third arguments, respectively, type fit.measures=TRUE and rsquare=TRUE to request the model fit indices and the unadjusted R² values for the endogenous variables.

# Print summary of model results
summary(srm_fit_full,        # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE,   # request standardized estimates
        rsquare=TRUE)        # request R-squared estimates

## lavaan 0.6.15 ended normally after 31 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        36
## 
##   Number of observations                           550
## 
## Model Test User Model:
##                                                       
##   Test statistic                               120.858
##   Degrees of freedom                               100
##   P-value (Chi-square)                           0.076
## 
## Model Test Baseline Model:
## 
##   Test statistic                              3851.181
##   Degrees of freedom                               120
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.994
##   Tucker-Lewis Index (TLI)                       0.993
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -12612.020
##   Loglikelihood unrestricted model (H1)     -12551.591
##                                                       
##   Akaike (AIC)                               25296.040
##   Bayesian (BIC)                             25451.197
##   Sample-size adjusted Bayesian (SABIC)      25336.918
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.019
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.031
##   P-value H_0: RMSEA <= 0.050                    1.000
##   P-value H_0: RMSEA >= 0.080                    0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.025
## 
## Parameter Estimates:
## 
##   Standard errors                            Bootstrap
##   Number of requested bootstrap draws             5000
##   Number of successful bootstrap draws            5000
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC =~                                                                 
##     RC1               1.000                               0.746    0.682
##     RC2               1.213    0.079   15.335    0.000    0.905    0.801
##     RC3               1.037    0.074   14.020    0.000    0.774    0.715
##     RC4               1.110    0.070   15.970    0.000    0.828    0.747
##   TM =~                                                                 
##     TM1               1.000                               0.923    0.783
##     TM2               1.051    0.060   17.495    0.000    0.970    0.783
##     TM3               0.998    0.053   18.795    0.000    0.921    0.801
##     TM4               0.985    0.057   17.288    0.000    0.909    0.753
##   JS =~                                                                 
##     JS1               1.000                               0.907    0.737
##     JS2               1.048    0.060   17.440    0.000    0.951    0.776
##     JS3               0.994    0.060   16.463    0.000    0.902    0.734
##     JS4               1.033    0.062   16.619    0.000    0.937    0.764
##   JP =~                                                                 
##     JP1               1.000                               1.168    0.766
##     JP2               1.102    0.058   19.036    0.000    1.288    0.801
##     JP3               0.981    0.054   18.121    0.000    1.146    0.794
##     JP4               0.994    0.059   16.963    0.000    1.161    0.752
## 
## Regressions:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   JS ~                                                                  
##     RC        (a1)    0.433    0.063    6.902    0.000    0.356    0.356
##     TM        (a2)    0.295    0.043    6.874    0.000    0.300    0.300
##   JP ~                                                                  
##     JS         (b)    0.501    0.064    7.842    0.000    0.389    0.389
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC ~~                                                                 
##     TM                0.087    0.036    2.425    0.015    0.127    0.127
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC1               0.639    0.050   12.741    0.000    0.639    0.535
##    .RC2               0.458    0.044   10.352    0.000    0.458    0.359
##    .RC3               0.571    0.043   13.325    0.000    0.571    0.488
##    .RC4               0.545    0.049   11.062    0.000    0.545    0.443
##    .TM1               0.538    0.048   11.186    0.000    0.538    0.387
##    .TM2               0.594    0.050   11.989    0.000    0.594    0.387
##    .TM3               0.472    0.043   10.929    0.000    0.472    0.358
##    .TM4               0.631    0.045   14.085    0.000    0.631    0.433
##    .JS1               0.693    0.051   13.714    0.000    0.693    0.457
##    .JS2               0.596    0.048   12.375    0.000    0.596    0.397
##    .JS3               0.696    0.051   13.586    0.000    0.696    0.461
##    .JS4               0.626    0.053   11.908    0.000    0.626    0.416
##    .JP1               0.960    0.078   12.362    0.000    0.960    0.413
##    .JP2               0.927    0.076   12.134    0.000    0.927    0.359
##    .JP3               0.771    0.064   11.983    0.000    0.771    0.370
##    .JP4               1.036    0.074   14.018    0.000    1.036    0.434
##     RC                0.556    0.062    8.917    0.000    1.000    1.000
##     TM                0.852    0.082   10.384    0.000    1.000    1.000
##    .JS                0.623    0.070    8.943    0.000    0.756    0.756
##    .JP                1.158    0.116   10.016    0.000    0.849    0.849
## 
## R-Square:
##                    Estimate
##     RC1               0.465
##     RC2               0.641
##     RC3               0.512
##     RC4               0.557
##     TM1               0.613
##     TM2               0.613
##     TM3               0.642
##     TM4               0.567
##     JS1               0.543
##     JS2               0.603
##     JS3               0.539
##     JS4               0.584
##     JP1               0.587
##     JP2               0.641
##     JP3               0.630
##     JP4               0.566
##     JS                0.244
##     JP                0.151
## 
## Defined Parameters:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     a1b               0.217    0.041    5.340    0.000    0.138    0.138
##     a2b               0.148    0.028    5.332    0.000    0.117    0.117

We are ready to apply and print the percentile bootrapping 95% confidence intervals to evaluate the statistical significance of the indirect effects we specified.

1. Type the name of the parameterEstimates function from the lavaan package.
2. As the first argument in the parameterEstimates function, insert the name of the fitted model object (srm_fit_full).
3. As the second argument, request confidence intervals using the ci=TRUE argument.
4. As the third argument, request 95% confidence intervals using the level=0.95 argument.
5. As the fourth argument, request percentile bootstrapping using the boot.ci.type="perc" argument.

# Request percentile bootstrap 95% confidence intervals
parameterEstimates(srm_fit_full,        # name of fitted model object
                   ci=TRUE,             # request confidence intervals
                   level=0.95,          # request 95% confidence intervals
                   boot.ci.type="perc") # request percentile bootstrapping

##    lhs op  rhs label   est    se      z pvalue ci.lower ci.upper
## 1   RC =~  RC1       1.000 0.000     NA     NA    1.000    1.000
## 2   RC =~  RC2       1.213 0.079 15.335  0.000    1.067    1.378
## 3   RC =~  RC3       1.037 0.074 14.020  0.000    0.898    1.193
## 4   RC =~  RC4       1.110 0.070 15.970  0.000    0.983    1.255
## 5   TM =~  TM1       1.000 0.000     NA     NA    1.000    1.000
## 6   TM =~  TM2       1.051 0.060 17.495  0.000    0.940    1.179
## 7   TM =~  TM3       0.998 0.053 18.795  0.000    0.900    1.108
## 8   TM =~  TM4       0.985 0.057 17.288  0.000    0.880    1.104
## 9   JS =~  JS1       1.000 0.000     NA     NA    1.000    1.000
## 10  JS =~  JS2       1.048 0.060 17.440  0.000    0.937    1.174
## 11  JS =~  JS3       0.994 0.060 16.463  0.000    0.880    1.118
## 12  JS =~  JS4       1.033 0.062 16.619  0.000    0.916    1.162
## 13  JP =~  JP1       1.000 0.000     NA     NA    1.000    1.000
## 14  JP =~  JP2       1.102 0.058 19.036  0.000    0.996    1.222
## 15  JP =~  JP3       0.981 0.054 18.121  0.000    0.880    1.092
## 16  JP =~  JP4       0.994 0.059 16.963  0.000    0.885    1.116
## 17  JS  ~   RC    a1 0.433 0.063  6.902  0.000    0.316    0.558
## 18  JS  ~   TM    a2 0.295 0.043  6.874  0.000    0.214    0.381
## 19  JP  ~   JS     b 0.501 0.064  7.842  0.000    0.382    0.631
## 20 RC1 ~~  RC1       0.639 0.050 12.741  0.000    0.542    0.736
## 21 RC2 ~~  RC2       0.458 0.044 10.352  0.000    0.373    0.545
## 22 RC3 ~~  RC3       0.571 0.043 13.325  0.000    0.487    0.655
## 23 RC4 ~~  RC4       0.545 0.049 11.062  0.000    0.448    0.640
## 24 TM1 ~~  TM1       0.538 0.048 11.186  0.000    0.446    0.636
## 25 TM2 ~~  TM2       0.594 0.050 11.989  0.000    0.496    0.690
## 26 TM3 ~~  TM3       0.472 0.043 10.929  0.000    0.387    0.558
## 27 TM4 ~~  TM4       0.631 0.045 14.085  0.000    0.545    0.720
## 28 JS1 ~~  JS1       0.693 0.051 13.714  0.000    0.590    0.793
## 29 JS2 ~~  JS2       0.596 0.048 12.375  0.000    0.501    0.690
## 30 JS3 ~~  JS3       0.696 0.051 13.586  0.000    0.597    0.798
## 31 JS4 ~~  JS4       0.626 0.053 11.908  0.000    0.525    0.729
## 32 JP1 ~~  JP1       0.960 0.078 12.362  0.000    0.808    1.109
## 33 JP2 ~~  JP2       0.927 0.076 12.134  0.000    0.776    1.074
## 34 JP3 ~~  JP3       0.771 0.064 11.983  0.000    0.644    0.893
## 35 JP4 ~~  JP4       1.036 0.074 14.018  0.000    0.885    1.174
## 36  RC ~~   RC       0.556 0.062  8.917  0.000    0.439    0.683
## 37  TM ~~   TM       0.852 0.082 10.384  0.000    0.694    1.014
## 38  JS ~~   JS       0.623 0.070  8.943  0.000    0.489    0.765
## 39  JP ~~   JP       1.158 0.116 10.016  0.000    0.939    1.390
## 40  RC ~~   TM       0.087 0.036  2.425  0.015    0.017    0.157
## 41 a1b := a1*b   a1b 0.217 0.041  5.340  0.000    0.144    0.302
## 42 a2b := a2*b   a2b 0.148 0.028  5.332  0.000    0.097    0.206

At the bottom of the output, you should see the indirect effects that we specified (a1b := a1*b and a2b := a2*b). The unstandardized estimate for the indirect effects appear in the est column of the output table. As you can, see the a1b indirect effect point estimate is positive (.217), and the lower limit of the 95% confidence interval is .144 and the upper limit is .302; given that the confidence interval does not include zero, we can conclude that the a1b indirect effect (RC > JS > JP) is statistically significantly different from zero, which provides evidence that JS mediates the association between RC and JP. The a2b indirect effect point estimate is also positive (.148), and the lower limit of the 95% confidence interval is .097 and the upper limit is .206; given that the confidence interval does not include zero, we can conclude that the a2b indirect effect (TM > JS > JP) is statistically significantly different from zero, which provides evidence that JS mediates the association between TM and JP. In sum, both indirect effects were statistically significant and positive in sign.

58.2.8 Estimating Models with Missing Data

When missing data are present, we must carefully consider how we handle the missing data before or during the estimations of a model. In the chapter on missing data, I provide an overview of relevant concepts, particularly if the data are missing completely at random (MCAR), missing at random (MAR), or missing not at random (MNAR); I suggest reviewing that chapter prior to handling missing data.

As a potential method for addressing missing data, the lavaan model functions, such as the sem function, allow for full-information maximum likelihood (FIML). Further, the functions allow us to specify specific estimators given the type of data we wish to use for model estimation (e.g., ML, MLR).

To demonstrate how missing data are handled using FIML, we will need to first introduce some missing data into our data. To do so, we will use a multiple imputation package called mice and a function called ampute that “amputates” existing data by creating missing data patterns. For our purposes, we’ll replace 10% (.1) of data frame cells with NA (which signifies a missing value) such that the missing data are missing completely at random (MCAR).

# Install package
install.packages("mice")

# Access package
library(mice)

# Create a new data frame object
df_missing <- df

# Remove non-numeric variable(s) from data frame object
df_missing$EmployeeID <- NULL

# Set a seed
set.seed(2024)

# Remove 10% of cells so missing data are MCAR
df_missing <- ampute(df_missing, prop=.1, mech="MCAR")

# Extract the new missing data frame object and overwrite existing object
df_missing <- df_missing$amp

Implementing FIML when missing data are present is relatively straightforward. For example, for a structural regression model (SRM) from a previous section, we can apply FIML in the presence of missing data by adding the missing="fiml" argument to the sem function.

# Specify four-factor SRM & assign to object
srm_mod <- "
# Measurement model
RC =~ RC1 + RC2 + RC3 + RC4
TM =~ TM1 + TM2 + TM3 + TM4
JS =~ JS1 + JS2 + JS3 + JS4
JP =~ JP1 + JP2 + JP3 + JP4

# Directional paths/relations
JS ~ RC + TM
JP ~ JS
"

# Estimate four-factor SRM model & assign to fitted model object
srm_fit <- sem(srm_mod,         # name of specified model object
               data=df_missing, # name of data frame object
               missing="fiml")  # specify FIML

# Print summary of model results
summary(srm_fit,             # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE,   # request standardized estimates
        rsquare=TRUE)        # request R-squared estimates

## lavaan 0.6.15 ended normally after 70 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        52
## 
##   Number of observations                           550
##   Number of missing patterns                        17
## 
## Model Test User Model:
##                                                       
##   Test statistic                               118.299
##   Degrees of freedom                               100
##   P-value (Chi-square)                           0.102
## 
## Model Test Baseline Model:
## 
##   Test statistic                              3817.668
##   Degrees of freedom                               120
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.995
##   Tucker-Lewis Index (TLI)                       0.994
##                                                       
##   Robust Comparative Fit Index (CFI)             0.995
##   Robust Tucker-Lewis Index (TLI)                0.994
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -12547.304
##   Loglikelihood unrestricted model (H1)     -12488.154
##                                                       
##   Akaike (AIC)                               25198.608
##   Bayesian (BIC)                             25422.723
##   Sample-size adjusted Bayesian (SABIC)      25257.653
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.018
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.030
##   P-value H_0: RMSEA <= 0.050                    1.000
##   P-value H_0: RMSEA >= 0.080                    0.000
##                                                       
##   Robust RMSEA                                   0.019
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.030
##   P-value H_0: Robust RMSEA <= 0.050             1.000
##   P-value H_0: Robust RMSEA >= 0.080             0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.025
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Observed
##   Observed information based on                Hessian
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC =~                                                                 
##     RC1               1.000                               0.746    0.683
##     RC2               1.223    0.081   15.038    0.000    0.912    0.804
##     RC3               1.035    0.074   14.021    0.000    0.772    0.715
##     RC4               1.110    0.075   14.735    0.000    0.827    0.745
##   TM =~                                                                 
##     TM1               1.000                               0.922    0.784
##     TM2               1.051    0.058   18.196    0.000    0.969    0.782
##     TM3               0.997    0.053   18.681    0.000    0.919    0.801
##     TM4               0.985    0.057   17.384    0.000    0.908    0.753
##   JS =~                                                                 
##     JS1               1.000                               0.911    0.738
##     JS2               1.038    0.064   16.252    0.000    0.945    0.775
##     JS3               0.984    0.063   15.726    0.000    0.896    0.731
##     JS4               1.033    0.062   16.553    0.000    0.940    0.767
##   JP =~                                                                 
##     JP1               1.000                               1.165    0.765
##     JP2               1.102    0.061   18.183    0.000    1.284    0.798
##     JP3               0.984    0.055   17.897    0.000    1.146    0.794
##     JP4               1.003    0.059   17.001    0.000    1.168    0.755
## 
## Regressions:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   JS ~                                                                  
##     RC                0.436    0.063    6.881    0.000    0.357    0.357
##     TM                0.298    0.048    6.227    0.000    0.302    0.302
##   JP ~                                                                  
##     JS                0.495    0.066    7.507    0.000    0.387    0.387
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC ~~                                                                 
##     TM                0.084    0.035    2.381    0.017    0.122    0.122
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC1               4.297    0.047   92.163    0.000    4.297    3.937
##    .RC2               4.386    0.049   90.438    0.000    4.386    3.867
##    .RC3               4.304    0.046   93.414    0.000    4.304    3.990
##    .RC4               4.197    0.047   88.542    0.000    4.197    3.779
##    .TM1               4.289    0.050   85.418    0.000    4.289    3.647
##    .TM2               4.295    0.053   81.263    0.000    4.295    3.468
##    .TM3               4.313    0.049   88.071    0.000    4.313    3.757
##    .TM4               4.307    0.052   83.532    0.000    4.307    3.570
##    .JS1               4.104    0.053   77.934    0.000    4.104    3.327
##    .JS2               4.115    0.052   79.045    0.000    4.115    3.375
##    .JS3               4.197    0.052   80.165    0.000    4.197    3.425
##    .JS4               4.103    0.052   78.418    0.000    4.103    3.345
##    .JP1               7.095    0.065  109.224    0.000    7.095    4.662
##    .JP2               7.083    0.069  103.168    0.000    7.083    4.405
##    .JP3               7.202    0.062  116.959    0.000    7.202    4.992
##    .JP4               7.082    0.066  107.182    0.000    7.082    4.577
##     RC                0.000                               0.000    0.000
##     TM                0.000                               0.000    0.000
##    .JS                0.000                               0.000    0.000
##    .JP                0.000                               0.000    0.000
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC1               0.636    0.047   13.562    0.000    0.636    0.534
##    .RC2               0.456    0.044   10.264    0.000    0.456    0.354
##    .RC3               0.568    0.044   13.004    0.000    0.568    0.488
##    .RC4               0.549    0.045   12.177    0.000    0.549    0.445
##    .TM1               0.533    0.044   12.215    0.000    0.533    0.385
##    .TM2               0.596    0.049   12.213    0.000    0.596    0.388
##    .TM3               0.473    0.041   11.665    0.000    0.473    0.359
##    .TM4               0.630    0.049   12.980    0.000    0.630    0.433
##    .JS1               0.693    0.054   12.890    0.000    0.693    0.455
##    .JS2               0.593    0.050   11.938    0.000    0.593    0.399
##    .JS3               0.698    0.054   12.999    0.000    0.698    0.465
##    .JS4               0.620    0.051   12.210    0.000    0.620    0.412
##    .JP1               0.960    0.076   12.712    0.000    0.960    0.414
##    .JP2               0.937    0.080   11.695    0.000    0.937    0.362
##    .JP3               0.769    0.065   11.835    0.000    0.769    0.369
##    .JP4               1.030    0.080   12.923    0.000    1.030    0.430
##     RC                0.556    0.066    8.359    0.000    1.000    1.000
##     TM                0.850    0.082   10.307    0.000    1.000    1.000
##    .JS                0.626    0.071    8.866    0.000    0.756    0.756
##    .JP                1.153    0.119    9.679    0.000    0.850    0.850
## 
## R-Square:
##                    Estimate
##     RC1               0.466
##     RC2               0.646
##     RC3               0.512
##     RC4               0.555
##     TM1               0.615
##     TM2               0.612
##     TM3               0.641
##     TM4               0.567
##     JS1               0.545
##     JS2               0.601
##     JS3               0.535
##     JS4               0.588
##     JP1               0.586
##     JP2               0.638
##     JP3               0.631
##     JP4               0.570
##     JS                0.244
##     JP                0.150

The FIML approach uses all observations in which data are missing on one or more endogenous observed variables in the model. As you can see in the output, all 550 observations were retained when estimating the model.

Now watch what happens when we remove the missing="fiml" argument in the presence of missing data.

# Specify four-factor SRM & assign to object
srm_mod <- "
# Measurement model
RC =~ RC1 + RC2 + RC3 + RC4
TM =~ TM1 + TM2 + TM3 + TM4
JS =~ JS1 + JS2 + JS3 + JS4
JP =~ JP1 + JP2 + JP3 + JP4

# Directional paths/relations
JS ~ RC + TM
JP ~ JS
"

# Estimate four-factor SRM model & assign to fitted model object
srm_fit <- sem(srm_mod,         # name of specified model object
               data=df_missing) # name of data frame object

# Print summary of model results
summary(srm_fit,             # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE,   # request standardized estimates
        rsquare=TRUE)        # request R-squared estimates

## lavaan 0.6.15 ended normally after 32 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        36
## 
##                                                   Used       Total
##   Number of observations                           505         550
## 
## Model Test User Model:
##                                                       
##   Test statistic                               123.540
##   Degrees of freedom                               100
##   P-value (Chi-square)                           0.055
## 
## Model Test Baseline Model:
## 
##   Test statistic                              3587.377
##   Degrees of freedom                               120
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.993
##   Tucker-Lewis Index (TLI)                       0.992
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -11560.579
##   Loglikelihood unrestricted model (H1)     -11498.809
##                                                       
##   Akaike (AIC)                               23193.158
##   Bayesian (BIC)                             23345.243
##   Sample-size adjusted Bayesian (SABIC)      23230.975
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.022
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.033
##   P-value H_0: RMSEA <= 0.050                    1.000
##   P-value H_0: RMSEA >= 0.080                    0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.027
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC =~                                                                 
##     RC1               1.000                               0.735    0.671
##     RC2               1.256    0.087   14.481    0.000    0.923    0.807
##     RC3               1.054    0.078   13.451    0.000    0.775    0.720
##     RC4               1.137    0.082   13.884    0.000    0.836    0.751
##   TM =~                                                                 
##     TM1               1.000                               0.917    0.784
##     TM2               1.075    0.060   17.881    0.000    0.986    0.795
##     TM3               1.002    0.055   18.054    0.000    0.918    0.803
##     TM4               0.999    0.059   17.019    0.000    0.916    0.758
##   JS =~                                                                 
##     JS1               1.000                               0.923    0.738
##     JS2               1.043    0.065   16.173    0.000    0.963    0.787
##     JS3               0.978    0.064   15.229    0.000    0.903    0.735
##     JS4               1.019    0.064   15.820    0.000    0.941    0.766
##   JP =~                                                                 
##     JP1               1.000                               1.147    0.754
##     JP2               1.125    0.066   17.117    0.000    1.290    0.804
##     JP3               0.978    0.058   16.840    0.000    1.122    0.788
##     JP4               1.011    0.063   16.099    0.000    1.160    0.752
## 
## Regressions:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   JS ~                                                                  
##     RC                0.452    0.068    6.669    0.000    0.360    0.360
##     TM                0.308    0.051    6.073    0.000    0.306    0.306
##   JP ~                                                                  
##     JS                0.497    0.067    7.388    0.000    0.400    0.400
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC ~~                                                                 
##     TM                0.088    0.036    2.446    0.014    0.130    0.130
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC1               0.658    0.050   13.299    0.000    0.658    0.549
##    .RC2               0.456    0.046    9.896    0.000    0.456    0.349
##    .RC3               0.558    0.045   12.456    0.000    0.558    0.482
##    .RC4               0.538    0.046   11.703    0.000    0.538    0.435
##    .TM1               0.528    0.044   11.881    0.000    0.528    0.386
##    .TM2               0.566    0.049   11.559    0.000    0.566    0.368
##    .TM3               0.465    0.041   11.311    0.000    0.465    0.355
##    .TM4               0.621    0.050   12.511    0.000    0.621    0.426
##    .JS1               0.715    0.057   12.536    0.000    0.715    0.456
##    .JS2               0.572    0.051   11.306    0.000    0.572    0.381
##    .JS3               0.696    0.055   12.598    0.000    0.696    0.460
##    .JS4               0.623    0.052   11.879    0.000    0.623    0.413
##    .JP1               0.996    0.080   12.392    0.000    0.996    0.431
##    .JP2               0.913    0.083   11.030    0.000    0.913    0.354
##    .JP3               0.766    0.067   11.510    0.000    0.766    0.378
##    .JP4               1.036    0.083   12.453    0.000    1.036    0.435
##     RC                0.541    0.069    7.876    0.000    1.000    1.000
##     TM                0.841    0.085    9.917    0.000    1.000    1.000
##    .JS                0.638    0.074    8.630    0.000    0.748    0.748
##    .JP                1.105    0.121    9.112    0.000    0.840    0.840
## 
## R-Square:
##                    Estimate
##     RC1               0.451
##     RC2               0.651
##     RC3               0.518
##     RC4               0.565
##     TM1               0.614
##     TM2               0.632
##     TM3               0.645
##     TM4               0.574
##     JS1               0.544
##     JS2               0.619
##     JS3               0.540
##     JS4               0.587
##     JP1               0.569
##     JP2               0.646
##     JP3               0.622
##     JP4               0.565
##     JS                0.252
##     JP                0.160

As you can see in the output, the sem function defaults to listwise deletion when we do not specify that FIML be applied. This results in the number of observations dropping from 550 to 505 for model estimation purposes. A reduction in sample size can negatively affect our statistical power to detect associations or effects that truly exist in the underlying population. To learn more about statistical power, please refer to the chapter on power analysis.

Within the sem function, we can also specify a specific estimator if we choose to override the default. For example, we could specify the MLR (maximum likelihood with robust standard errors) estimator if we had good reason to. To do so, we would add this argument: estimator="MLR". For a list of other available estimators, you can check out the lavaan package website.

# Specify four-factor SRM & assign to object
srm_mod <- "
# Measurement model
RC =~ RC1 + RC2 + RC3 + RC4
TM =~ TM1 + TM2 + TM3 + TM4
JS =~ JS1 + JS2 + JS3 + JS4
JP =~ JP1 + JP2 + JP3 + JP4

# Directional paths/relations
JS ~ RC + TM
JP ~ JS
"

# Estimate four-factor SRM model & assign to fitted model object
srm_fit <- sem(srm_mod,         # name of specified model object
               data=df_missing, # name of data frame object
               estimator="MLR", # request MLR estimator
               missing="fiml")  # specify FIML

# Print summary of model results
summary(srm_fit,             # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE,   # request standardized estimates
        rsquare=TRUE)        # request R-squared estimates

## lavaan 0.6.15 ended normally after 70 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        52
## 
##   Number of observations                           550
##   Number of missing patterns                        17
## 
## Model Test User Model:
##                                               Standard      Scaled
##   Test Statistic                               118.299     117.571
##   Degrees of freedom                               100         100
##   P-value (Chi-square)                           0.102       0.111
##   Scaling correction factor                                  1.006
##     Yuan-Bentler correction (Mplus variant)                       
## 
## Model Test Baseline Model:
## 
##   Test statistic                              3817.668    3786.218
##   Degrees of freedom                               120         120
##   P-value                                        0.000       0.000
##   Scaling correction factor                                  1.008
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.995       0.995
##   Tucker-Lewis Index (TLI)                       0.994       0.994
##                                                                   
##   Robust Comparative Fit Index (CFI)                         0.995
##   Robust Tucker-Lewis Index (TLI)                            0.994
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -12547.304  -12547.304
##   Scaling correction factor                                  0.976
##       for the MLR correction                                      
##   Loglikelihood unrestricted model (H1)     -12488.154  -12488.154
##   Scaling correction factor                                  0.996
##       for the MLR correction                                      
##                                                                   
##   Akaike (AIC)                               25198.608   25198.608
##   Bayesian (BIC)                             25422.723   25422.723
##   Sample-size adjusted Bayesian (SABIC)      25257.653   25257.653
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.018       0.018
##   90 Percent confidence interval - lower         0.000       0.000
##   90 Percent confidence interval - upper         0.030       0.030
##   P-value H_0: RMSEA <= 0.050                    1.000       1.000
##   P-value H_0: RMSEA >= 0.080                    0.000       0.000
##                                                                   
##   Robust RMSEA                                               0.018
##   90 Percent confidence interval - lower                     0.000
##   90 Percent confidence interval - upper                     0.030
##   P-value H_0: Robust RMSEA <= 0.050                         1.000
##   P-value H_0: Robust RMSEA >= 0.080                         0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.025       0.025
## 
## Parameter Estimates:
## 
##   Standard errors                             Sandwich
##   Information bread                           Observed
##   Observed information based on                Hessian
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC =~                                                                 
##     RC1               1.000                               0.746    0.683
##     RC2               1.223    0.080   15.228    0.000    0.912    0.804
##     RC3               1.035    0.073   14.146    0.000    0.772    0.715
##     RC4               1.110    0.071   15.729    0.000    0.827    0.745
##   TM =~                                                                 
##     TM1               1.000                               0.922    0.784
##     TM2               1.051    0.061   17.243    0.000    0.969    0.782
##     TM3               0.997    0.053   18.966    0.000    0.919    0.801
##     TM4               0.985    0.056   17.436    0.000    0.908    0.753
##   JS =~                                                                 
##     JS1               1.000                               0.911    0.738
##     JS2               1.038    0.059   17.491    0.000    0.945    0.775
##     JS3               0.984    0.059   16.586    0.000    0.896    0.731
##     JS4               1.033    0.062   16.715    0.000    0.940    0.767
##   JP =~                                                                 
##     JP1               1.000                               1.165    0.765
##     JP2               1.102    0.058   18.953    0.000    1.284    0.798
##     JP3               0.984    0.054   18.118    0.000    1.146    0.794
##     JP4               1.003    0.060   16.852    0.000    1.168    0.755
## 
## Regressions:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   JS ~                                                                  
##     RC                0.436    0.062    6.973    0.000    0.357    0.357
##     TM                0.298    0.043    6.968    0.000    0.302    0.302
##   JP ~                                                                  
##     JS                0.495    0.064    7.730    0.000    0.387    0.387
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   RC ~~                                                                 
##     TM                0.084    0.036    2.313    0.021    0.122    0.122
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC1               4.297    0.047   92.145    0.000    4.297    3.937
##    .RC2               4.386    0.049   90.439    0.000    4.386    3.867
##    .RC3               4.304    0.046   93.389    0.000    4.304    3.990
##    .RC4               4.197    0.047   88.536    0.000    4.197    3.779
##    .TM1               4.289    0.050   85.408    0.000    4.289    3.647
##    .TM2               4.295    0.053   81.263    0.000    4.295    3.468
##    .TM3               4.313    0.049   88.066    0.000    4.313    3.757
##    .TM4               4.307    0.052   83.531    0.000    4.307    3.570
##    .JS1               4.104    0.053   77.930    0.000    4.104    3.327
##    .JS2               4.115    0.052   79.048    0.000    4.115    3.375
##    .JS3               4.197    0.052   80.168    0.000    4.197    3.425
##    .JS4               4.103    0.052   78.426    0.000    4.103    3.345
##    .JP1               7.095    0.065  109.231    0.000    7.095    4.662
##    .JP2               7.083    0.069  103.194    0.000    7.083    4.405
##    .JP3               7.202    0.062  116.945    0.000    7.202    4.992
##    .JP4               7.082    0.066  107.182    0.000    7.082    4.577
##     RC                0.000                               0.000    0.000
##     TM                0.000                               0.000    0.000
##    .JS                0.000                               0.000    0.000
##    .JP                0.000                               0.000    0.000
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC1               0.636    0.050   12.828    0.000    0.636    0.534
##    .RC2               0.456    0.045   10.115    0.000    0.456    0.354
##    .RC3               0.568    0.043   13.362    0.000    0.568    0.488
##    .RC4               0.549    0.050   11.010    0.000    0.549    0.445
##    .TM1               0.533    0.048   11.159    0.000    0.533    0.385
##    .TM2               0.596    0.049   12.209    0.000    0.596    0.388
##    .TM3               0.473    0.044   10.818    0.000    0.473    0.359
##    .TM4               0.630    0.046   13.829    0.000    0.630    0.433
##    .JS1               0.693    0.051   13.640    0.000    0.693    0.455
##    .JS2               0.593    0.047   12.663    0.000    0.593    0.399
##    .JS3               0.698    0.052   13.424    0.000    0.698    0.465
##    .JS4               0.620    0.053   11.750    0.000    0.620    0.412
##    .JP1               0.960    0.078   12.304    0.000    0.960    0.414
##    .JP2               0.937    0.077   12.135    0.000    0.937    0.362
##    .JP3               0.769    0.064   11.984    0.000    0.769    0.369
##    .JP4               1.030    0.075   13.804    0.000    1.030    0.430
##     RC                0.556    0.063    8.824    0.000    1.000    1.000
##     TM                0.850    0.083   10.295    0.000    1.000    1.000
##    .JS                0.626    0.071    8.789    0.000    0.756    0.756
##    .JP                1.153    0.116    9.924    0.000    0.850    0.850
## 
## R-Square:
##                    Estimate
##     RC1               0.466
##     RC2               0.646
##     RC3               0.512
##     RC4               0.555
##     TM1               0.615
##     TM2               0.612
##     TM3               0.641
##     TM4               0.567
##     JS1               0.545
##     JS2               0.601
##     JS3               0.535
##     JS4               0.588
##     JP1               0.586
##     JP2               0.638
##     JP3               0.631
##     JP4               0.570
##     JS                0.244
##     JP                0.150

58.2.9 Summary

In this chapter, we learned how to estimate structural regression models using structural equation modeling, compare the fit of nested models, estimate indirect effects for mediation models, and estimate models when missing data are present.

References

Bagozzi, Richard P, and Youjae Yi. 1988. “On the Evaluation of Structural Equation Models.” Journal of the Academy of Marketing Science 16: 74–94.

Bentler, Peter M. 1968. “Alpha-Maximized Factor Analysis (Alphamax): Its Relation to Alpha and Canonical Factor Analysis.” Psychometrika 33 (3): 335–45.

Fornell, Claes, and David F Larcker. 1981. “Evaluating Structural Equation Models with Unobservable Variables and Measurement Errors.” Journal of Marketing Research 18 (1): 39–50.

Hu, Li-tze, and Peter M Bentler. 1999. “Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria Versus New Alternatives.” Structural Equation Modeling 6 (1): 1–55.

Kline, Rex B. 2011. Principles and Practice of Structural Equation Modeling (3rd Ed.). New York, New York: The Guilford Press.

McNeish, Daniel, and Melissa G Wolf. 2023. “Dynamic Fit Index Cutoffs for Confirmatory Factor Analysis Models.” Psychological Methods 28 (1): 61–88.

Nye, Christopher D. 2023. “Reviewer Resources: Confirmatory Factor Analysis.” Organizational Research Methods 26 (4): 608–28.

Wickham, Hadley, Jim Hester, and Jennifer Bryan. 2024. Readr: Read Rectangular Text Data. https://CRAN.R-project.org/package=readr.