Chapter 59 Estimating Change Using Latent Growth Modeling

In this chapter, we will learn how to estimate change using latent growth modeling (LGM), which is part of the structural equation modeling (SEM) family of analyses. Specifically, we will learn how to estimate change trajectories to understand new employees’ adjustment into an organization.

59.1 Conceptual Overview

Latent growth modeling (LGM) (or latent growth model (LGM)) is a latent variable modeling approach and is part of the structural equation modeling (SEM) family of analyses (Meredith and Tisak 1990). LGM also goes by other names such as latent curve analysis, latent growth curve modeling, or latent curve modeling. LGM is a useful statistical tool for estimating the extent to which employees’ levels of a particular construct change over time. Specifically, LGM helps us understand the functional form of change (e.g., linear, quadratic, cubic) and variation in change between employees. Although not the focus of this chapter, measurement models can be integrated into LGM through the implementation of confirmatory factor analysis (CFA); CFA was introduced in a previous chapter. For a comprehensive introduction to LGM (as well as other types of longitudinal SEM, e.g., latent state-trait models, growth mixture models), I recommend checking out the following book by Newsom (2024).

Newsom, J. T. (2024). Longitudinal structural equation modeling: A comprehensive introduction (2nd ed.). New York, NY: Routledge

In LGM, the intercept (or initial value) and slope (or functional form of change) are represented as latent variables (i.e., latent factors), which by nature are not directly measured. Instead, observed (manifest) variables serve as indicators of the latent factors. Further, the intercept and slopes latent factors provide information about the average intercept and slope for the population, as well as the between-person variation for the intercept and slope.

59.1.1 Path Diagrams

It is often helpful to visualize an LGM using a path diagram. A path diagram displays the model parameter specifications and can also include parameter estimates. Conventional path diagram symbols are shown in Figure 1.

Figure 1: Conventional path diagram symbols and their meanings.

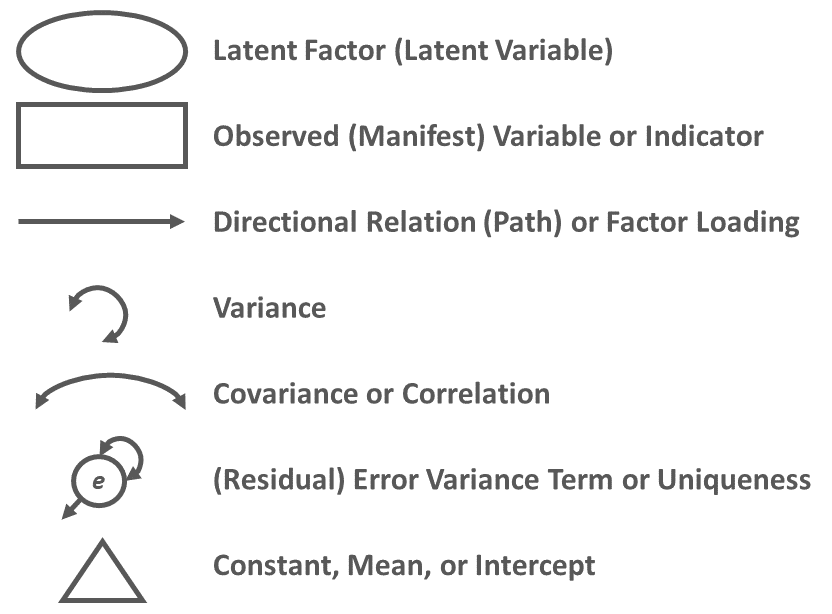
For an example of how the path diagram symbols can be used to construct a visual depiction of an LGM, please reference Figure 2. The path diagram depicts an unconditional unconstrained LGM with composite role clarity (RC) variables as observed measures (i.e., indicators), which means that the following parameters are freely estimated: means and variances for the intercept and slope latent factors, covariance between the intercept and slope latent factors, and variances for the observed variables. The model is considered unconditional because it is not conditioned on another variable, such as a time-invariant predictor variable. Further, role clarity (RC) measured at 1-month, 3-months, 6-months, and 9-months post-start-date serve as observed variables (i.e., RC 1m, RC 3m, RC 6m, RC 9m, respectively). That is, the RC observed measures serve as indicators of the intercept and slope latent factors, such that the indicators are reflective of the latent factors. Putting it all together, the unconditional unconstrained LGM can offer a glimpse into (a) whether employees’ levels of role clarity change on average in a particular direction (i.e., increase, decrease, no change) and (b) whether employees’ vary in terms of how their role clarity changes (if at all).

Figure 2: Example of an unconditional unconstrained LGM path diagram.

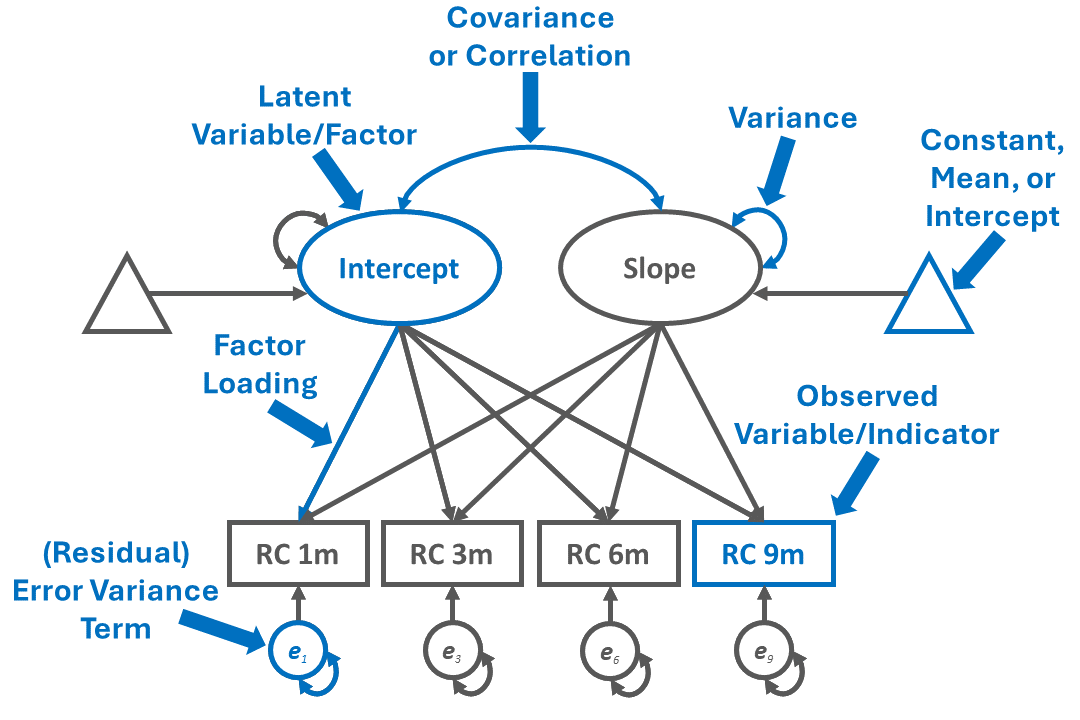
By convention, the latent factors for the role clarity intercept and slope are represented by an oval or circle. Please note that the latent factor is not directly measured; rather, we infer information about the latent factor from its four indicators, which in this example correspond to the four measurement occasions for role clarity.

The intercept and slope latent factors have variance terms associated with them, which represent the latent factors’ variabilities; these variances terms, which are represented by double-headed arrows, reflect the extent to which the intercept and slope estimates vary between individuals.

The intercept and slope latent factors also have mean (i.e., intercept, constant) terms associated with them, which are represented by triangles; these means reflect the average intercept and slope for the population.

The association between the intercept and slope latent factors is depicted using the double-headed arrow, which is referred to as a covariance – or if standardized, a correlation.

Each of the four observed variables (indicators) is represented with a rectangle. The one-directional, single-sided arrows extending from the latent factors to the observed variables represent the factor loadings. Each indicator has a (residual) error variance term, which represents the amount of variance left unexplained by the latent factor in relation to each indicator.

59.1.2 Model Identification

Model identification has to do with the number of (free or freely estimated) parameters specified in the model relative to the number of unique (non-redundant) sources of information available, and model implication has important implications for assessing model fit and estimating parameter estimates.

Just-identified: In a just-identified model (i.e., saturated model), the number of freely estimated parameters (e.g., factor loadings, covariances, variances) is equal to the number of unique (non-redundant) sources of information, which means that the degrees of freedom (df) is equal to zero. In just-identified models, the model parameter standard errors can be estimated, but the model fit cannot be assessed in a meaningful way using traditional model fit indices.

Over-identified: In an over-identified model, the number of freely estimated parameters is less than the number of unique (non-redundant) sources of information, which means that the degrees of freedom (df) is greater than zero. In over-identified models, traditional model fit indices and parameter standard errors can be estimated.

Under-identified: In an under-identified model, the number of freely estimated parameters is greater than the number of unique (non-redundant) sources of information, which means that the degrees of freedom (df) is less than zero. In under-identified models, the model parameter standard errors and model fit cannot be estimated. Some might say under-identified models are overparameterized because they have more parameters to be estimated than unique sources of information.

Most (if not all) statistical software packages that allow structural equation modeling (and by extension, latent growth modeling) automatically compute the degrees of freedom for a model or, if the model is under-identified, provide an error message. As such, we don’t need to count the number of sources of unique (non-redundant) sources of information and free parameters by hand. With that said, to understand model identification and its various forms at a deeper level, it is often helpful to practice calculating the degrees freedom by hand when first learning.

The formula for calculating the number of unique (non-redundant) sources of information available for a particular model is as follows, which differs from the formula for confirmatory factor analysis and other structural equation models because it incorporates repeated measurement occasions over time:

\(i = \frac{p(p+1)}{2} + t\)

where \(p\) is the number of observed variables to be modeled, and \(t\) is the number of measurement occasions (i.e., time points).

In unconditional unconstrained path diagram specified above, there are four observed variables: RC 1m, RC 3m, RC 6m, and RC 9m. Accordingly, in the following formula, \(p\) is equal to 4. There are four measurement occasions (i.e., 1 month, 3 months, 6 months, 9 months), so \(t\) is equal to 4. Thus, the number of unique (non-redundant) sources of information is 14.

\(i = \frac{4(4+1)}{2} + t = \frac{20}{2} + 4 = 14\)

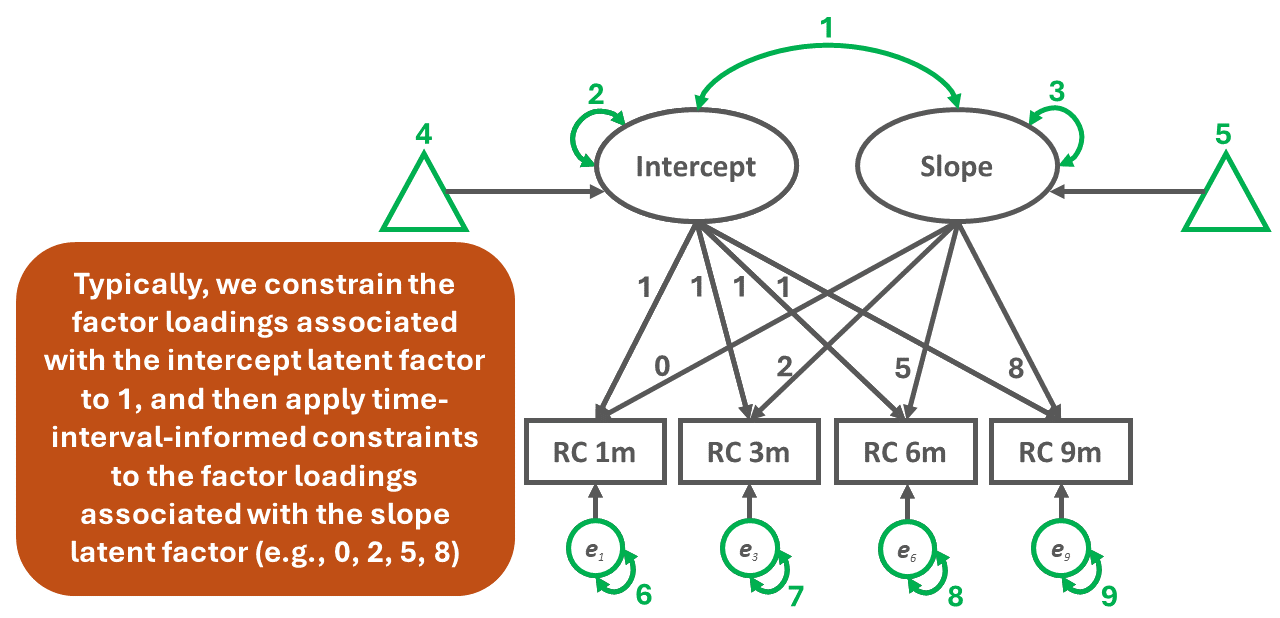
To count the number of free parameters (\(k\)), simply add up the number of the specified unconstrained factor loadings, variances, means, intercepts, covariances, and (residual) error variance terms in the unconditional unconstrained LGM. Please note that for latent factor scaling and time coding purposes, we typically (a) constrain all of the factor loadings associated with the intercept latent factor to 1.0 and (b) constrain the factor loadings associated with the slope latent factor to values that represent the time intervals (e.g., 0, 2, 5, 8), where zero represents the value of role clarity where the slope crosses the intercept. Had there been equal intervals for the measurement occasions for role clarity, we could have scaled the slope latent factor with factor loadings equal to 0, 1, 2, and 3; however, because the interval between RC 1m (1 month) and RC 3m (3 months) is not equal to the intervals between the other adjacent measurement occasions, we need to adjust the factor loadings by, in this instance, subtracting 1 from each measurement occasion month, so that RC 1m has a factor loading of 0, RC 3m has a factor loading of 2, RC 6m has a factor loading of 5, and RC 9m has a factor loading of 8. As shown in Figure 3 below, the example unconditional unconstrained LGM has 9 free parameters.

\(k = 9\)

To calculate the degrees of freedom (df) for the model, we need to subtract the number of free parameters from the number unique (non-redundant) sources of information, which in this example equates to 14 minus 9. Thus, the degrees of freedom for the model is 5, which means the model is over-identified.

\(df = i - k = 14 - 9 = 5\)

Figure 3: Counting the number of free parameters in the CFA model path diagram.

59.1.3 Model Fit

When a model is over-identified (df > 0), the extent to which the specified model fits the data can be assessed using a variety of model fit indices, such as the chi-square (\(\chi^{2}\)) test, comparative fit index (CFI), Tucker-Lewis index (TLI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR). As noted by Newsom, in the context of an LGM, these model fit indices reflect the amount of error around estimated slopes, and a poorly fitted model does not necessarily imply the absence of change over time or the accuracy of the functional form of change. For a commonly cited reference on cutoffs for fit indices, please refer to Hu and Bentler (1999), and for a concise description of common guidelines regarding interpreting model fit indices, including differences between stringent and relaxed interpretations of common fit indices, I recommend checking out Nye (2023). With that being said, those papers focus on confirmatory factor analyses as opposed to LGM. Regardless of which cutoffs we apply when interpreting fit indices, we must remember that such cutoffs are merely guidelines, and it’s possible to estimate an acceptable model that meets some but not all of the cutoffs given the limitations of some fit indices.

Chi-square test. The chi-square (\(\chi^{2}\)) test can be used to assess whether the model fits the data adequately, where a statistically significant \(\chi^{2}\) value (e.g., p \(<\) .05) indicates that the model does not fit the data well and a nonsignificant chi-square value (e.g., p \(\ge\) .05) indicates that the model fits the data reasonably well (Bagozzi and Yi 1988). The null hypothesis for the \(\chi^{2}\) test is that the model fits the data perfectly, and thus failing to reject the null model provides some confidence that the model fits the data reasonably close to perfectly. Of note, the \(\chi^{2}\) test is sensitive to sample size and non-normal variable distributions.

Comparative fit index (CFI). As the name implies, the comparative fit index (CFI) is a type of comparative (or incremental) fit index, which means that CFI compares the focal model to a baseline model, which is commonly referred to as the null or independence model. CFI is generally less sensitive to sample size than the chi-square test. A CFI value greater than or equal to .95 generally indicates good model fit to the data, although some might relax that cutoff to .90.

Tucker-Lewis index (TLI). Like CFI, Tucker-Lewis index (TLI) is another type of comparative (or incremental) fit index. TLI is generally less sensitive to sample size than the chi-square test and tends to work well with smaller sample sizes; however, as Hu and Bentler (1999) noted, TLI may be not be the best choice for smaller sample sizes (e.g., N \(<\) 250). A TLI value greater than or equal to .95 generally indicates good model fit to the data, although some might relax that cutoff to .90.

Root mean square error of approximation (RMSEA). The root mean square error of approximation (RMSEA) is an absolute fit index that penalizes model complexity (e.g., models with a larger number of estimated parameters) and thus ends up effectively rewarding more parsimonious models. RMSEA values tend to upwardly biased when the model degrees of freedom are fewer (i.e., when the model is closer to being just-identified); further, Hu and Bentler (1999) noted that RMSEA may not be the best choice for smaller sample sizes (e.g., N \(<\) 250). In general, an RMSEA value that is less than or equal to .06 indicates good model fit to the data, although some relax that cutoff to .08 or even .10.

Standardized root mean square residual (SRMR). Like the RMSEA, the standardized root mean square residual (SRMR) is an example of an absolute fit index. An SRMR value that is less than or equal to .06 generally indicates good fit to the data, although some relax that cutoff to .08.

Summary of model fit indices. The conventional cutoffs for the aforementioned model fit indices – like any rule of thumb – should be applied with caution and with good judgment and intention. Further, these indices don’t always agree with one another, which means that we often look across multiple fit indices and come up with our best judgment of whether the model adequately fits the data. A poorly fitting model may be due to model misspecification, an inappropriate model estimator, a large amount of error around slope estimates, or other factors that need to be addressed. With that being said, we should also be careful to not toss out a model entirely if one or more of the model fit indices suggest less than acceptable levels of fit to the data. The table below contains the conventional stringent and more relaxed cutoffs for the model fit indices.

Fit Index	Stringent Cutoffs for Acceptable Fit	Relaxed Cutoffs for Acceptable Fit
\(\chi^{2}\)	\(p \ge .05\)	\(p \ge .01\)
CFI	\(\ge .95\)	\(\ge .90\)
TLI	\(\ge .95\)	\(\ge .90\)
RMSEA	\(\le .06\)	\(\le .08\)
SRMR	\(\le .06\)	\(\le .08\)

59.1.4 Parameter Estimates

In LGM, there are various types of parameter estimates, which correspond to the path diagram symbols covered earlier (e.g., covariance, variance, mean, factor loading). When a model is just-identified or over-identified, we can estimate the standard errors for freely estimated parameters, which allows us to evaluate statistical significance. With most software applications, we can request standardized parameter estimates, which can facilitate the interpretation of some parameters.

Factor loadings. In LGM, it is common to apply constraints to all factor loadings extending from the intercept and slope latent factors to the observed variables; with that said, we can freely estimate some factor loadings associated with the slope factor, but a discussion of that topic is beyond the scope of this introductory chapter. For our purposes, we will constrain all factor loadings associated with the intercept latent factor to 1, whereas the factor loadings associated with the slope latent factor will reflect the intervals between measurement occasions (i.e., time coding). If we were to have four measurement occasions with equally spaced time intervals between adjacent occasions, then we could apply the following factor loadings to the slope factor: 0, 1, 2, and 3. Note, however, that we have a great deal of freedom when it comes to constraining the slope factor loadings, and the factor loading that we constrain to zero represents the value of our construct (e.g., role clarity) where the slope crosses the intercept. Alternatively, we could constrain our slope factor loadings as -3, -2, -1, and 0 if our goal were to estimate the intercept as the last measurement occasion. With respect to the LGM path diagram that has been our focus thus far (see Figure 2), we constrained our slope factor loadings to 0, 2, 5, and 8 because the intervals is not equal between adjacent measurement occasions. Namely, the interval between the 1-month and 3-months role clarity measurement occasions is 2 months (3 - 1 = 2), whereas the intervals between all other adjacent measurement occasions is 3 months (6 - 3 = 3 and 9 - 6 = 3). To account for the unequal intervals, I simply subtracted one from each measurement occasion month to arrive at the 0, 2, 5, and 8 factor loadings.

Variances. The variances of the latent factors represent the amount of between-person variability associated with intercept and slope estimates. A significant and large variance associated with the intercept latent factor suggests that individuals’ intercept estimates vary considerably from one another, whereas a significant or large variance associated with the slope latent factor suggests that individuals’ slope estimates vary considerably from one another.

Means. The means of the latent factors represent the average intercept and slope estimates. For example, with respect to the slope factor, a significant and positive mean indicates that, on average, individuals’ slopes were positive (e.g., increase in the measured construct over time), a nonsignificant mean indicates that, on average, individuals’ slopes were approximately zero (e.g., no change in the measured construct over time), and a significant and negative mean indicates that, on average, individuals’ slopes were negative (e.g., decrease in the measured construct over time).

Covariances. The covariance between the latent factors help us understand the extent to which intercept estimates are associated with slope estimates. For example, a negative covariance between the intercept and slope latent factors indicates that individuals who have higher intercept estimates tend to less positive slope estimates, whereas a positive covariance indicates that individuals who have higher intercept estimates tend to have more positive slope estimates. When standardized, a covariance can be interpreted as a correlation.

(Residual) error variance terms. The (residual) error variance terms, which are also known as disturbance terms or uniquenesses, indicate how much variance is left unexplained by the latent factors in relation to the observed variables (indicators). When standardized, error variance terms represent the proportion (percentage) of variance that remains unexplained by the latent factors.

59.1.5 Model Comparisons

When evaluating an LGM, we may wish to evaluate whether a focal LGM performs better (or worse) than an alternative LGM. Comparing models can help us arrive at a more parsimonious model that still fits the data well, as well as help us understand the extent to which construct demonstrates measurement invariance (or measurement equivalence) over time.

As an example, imagine we are focusing on our unconditional unconstrained LGM for role clarity (see Figure 2). Now imagine that we specify an alternative model in which we constrain the (residual) error variances to be equal, which could be used as a test for homogeneity of error variances. We can compare those two models to determine whether the alternative model fits the data about the same as our focal model or worse.

When two models are nested, we can perform nested model comparisons. As a reminder, a nested model has all the same parameter estimates of a full model but has additional parameter constraints in place. If two models are nested, we can compare them using model fit indices like CFI, TLI, RMSEA, and SRMR. We can also use the chi-square difference (\(\Delta \chi^{2}\)) test (likelihood ratio test) to compare nested models, which provides a statistical test for nested-model comparisons.

When two models are not nested, we can use other model fit indices like Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). With respect to these indices, the best fitting model will have lower AIC and BIC values.

59.1.6 Statistical Assumptions

The statistical assumptions that should be met prior to estimating and/or interpreting an LGM will depend on the type of estimation method. Common estimation methods for an LGM include (but are not limited to) maximum likelihood (ML), maximum likelihood with robust standard errors (MLM or MLR), weighted least squares (WLS), and diagonally weighted least squares (DWLS). WLS and DWLS estimation methods are used when there are observed variables with nominal or ordinal (categorical) measurement scales. In this chapter, we will focus on ML estimation, which is a common method when observed variables have interval or ratio (continuous) measurement scales. As Kline (2011) notes, ML estimation carries with it the following assumptions: “The statistical assumptions of ML estimation include independence of the scores, multivariate normality of the endogenous variables, and independence of the exogenous variables and error terms” (p. 159). When multivariate non-normality is a concern, the MLM or MLR estimator is a better choice than ML estimator, where the MLR estimator allows for missing data and the MLM estimator does not.

59.1.6.1 Sample Write-Up

As part of a new-employee onboarding longitudinal study, surveys were administered 1 month, 3 months, 6 months, and 9 months after employees’ respective start dates. Each survey included a 15-item measure of role clarity, and a composite variable based on the employees’ average responses was created at each survey measurement occasion. Using an unconditional unconstrained latent growth model (LGM), we investigated whether new employees’ levels of role clarity showed linear change over time and whether role-clarity change varied between new employees. When specifying the model, we constrained the intercept factor loadings to 1, and constrained the slope factor loadings to 0, 2, 5, and 8 to account for the unequal time intervals between adjacent measurement occasions. We estimated the model using the maximum likelihood (ML) estimator and a sample size of 650 new employees. Missing data were not a concern. We evaluated the model’s fit to the data using the chi-square (\(\chi^{2}\)) test, CFI, TLI, RMSEA, and SRMR model fit indices. The \(\chi^{2}\) test indicated that the model fit the data as well as a perfectly fitting model (\(\chi^{2}\) = 3.760 df = 5, p = .584). Further, the CFI and TLI estimates were 1.000 and 1.001, respectively, which exceeded the more stringent threshold of .95, thereby indicating that model showed acceptable fit to the data. Similarly, the RMSEA estimate was .00, which was below the more stringent threshold of .06, thereby indicating that model showed acceptable fit to the data. The SRMR estimate was .019, which was below the stringent threshold of .06, thereby indicating acceptable model fit to the data. Collectively, the model fit information indicated that model fit the data acceptably.

Regarding the unstandardized parameter estimates, the intercept latent factor mean of 35.143 (p < .001) indicated that, on average, new employees’ level of role clarity was 35.143 (out of a possible 100) 1 month after their respective start dates. The slope latent factor mean of 4.975 (p < .001) indicated that, on average, new employees’ level of role clarity increased by 4.975 each month. The variances associated with the intercept and slope latent factors, however, indicated that there was a statistically significant amount of between-employee intercept and slope variation (\(\sigma_{intercept}\) = 155.324, p < .001; \(\sigma_{slope}\) = .744, p < .001). The statistically significant and negative covariance between the intercept and slope latent factors indicated that employees with higher levels of role clarity 1 month after their respective start dates tended to have less positive role clarity change trajectories (\(\psi\) = -3.483, p = .002). Finally, the standardized (residual) error terms associated with the four observed role clarity measurement occasions ranged from .307 to .368, indicating that a proportionally small amount of variance was left unexplained by the intercept and slope latent factors.

In sum, the estimated unconditional constrained LGM showed that new employees’ role clarity, on average, increased in a linear manner between 1 month and 9 months after employees’ respective start dates. Further, new employees varied with respect to their level of role clarity 1 month after their start dates, and their role clarity change trajectories varied in terms of slope. A conditional model with a time-invariant predictor or time-variant predictors may help explain between-employee differences in intercepts and slopes.

59.2 Tutorial

This chapter’s tutorial demonstrates how to estimate change using latent growth modeling (LGM) in R.

59.2.1 Video Tutorial

The video tutorial for this chapter is planned but has not yet been recorded.

59.2.2 Functions & Packages Introduced

Function	Package
pivot_longer	tidyr
mutate	dplyr
case_match	dplyr
ggplot	ggplot2
aes	ggplot2
geom_line	ggplot2
labs	ggplot2
scale_x_continuous	ggplot2
theme_classic	ggplot2
slice	dplyr
growth	lavaan
summary	base R
semPaths	semPlot
anova	base R
options	base R
inspect	lavaan
cbind	base R
rbind	base R
t	base R
ampute	mice

59.2.3 Initial Steps

If you haven’t already, save the file called “lgm.csv” into a folder that you will subsequently set as your working directory. Your working directory will likely be different than the one shown below (i.e., "H:/RWorkshop"). As a reminder, you can access all of the data files referenced in this book by downloading them as a compressed (zipped) folder from the my GitHub site: https://github.com/davidcaughlin/R-Tutorial-Data-Files; once you’ve followed the link to GitHub, just click “Code” (or “Download”) followed by “Download ZIP”, which will download all of the data files referenced in this book. For the sake of parsimony, I recommend downloading all of the data files into the same folder on your computer, which will allow you to set that same folder as your working directory for each of the chapters in this book.

Next, using the setwd function, set your working directory to the folder in which you saved the data file for this chapter. Alternatively, you can manually set your working directory folder in your drop-down menus by going to Session > Set Working Directory > Choose Directory…. Be sure to create a new R script file (.R) or update an existing R script file so that you can save your script and annotations. If you need refreshers on how to set your working directory and how to create and save an R script, please refer to Setting a Working Directory and Creating & Saving an R Script.

# Set your working directory
setwd("H:/RWorkshop")

Next, read in the .csv data file called “lgm.csv” using your choice of read function. In this example, I use the read_csv function from the readr package (Wickham, Hester, and Bryan 2024). If you choose to use the read_csv function, be sure that you have installed and accessed the readr package using the install.packages and library functions. Note: You don’t need to install a package every time you wish to access it; in general, I would recommend updating a package installation once ever 1-3 months. For refreshers on installing packages and reading data into R, please refer to Packages and Reading Data into R.

# Install readr package if you haven't already
# [Note: You don't need to install a package every 
# time you wish to access it]
install.packages("readr")

# Access readr package
library(readr)

# Read data and name data frame (tibble) object
df <- read_csv("lgm.csv")

## Rows: 650 Columns: 7
## ── Column specification ────────────────────────────────────────────────────────────────────────────────────────────────────────────
## Delimiter: ","
## chr (1): EmployeeID
## dbl (6): RC_1m, RC_3m, RC_6m, RC_9m, ProPers_d1, JobPerf_12m
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

# Print the names of the variables in the data frame (tibble) object
names(df)

## [1] "EmployeeID"  "RC_1m"       "RC_3m"       "RC_6m"       "RC_9m"       "ProPers_d1"  "JobPerf_12m"

# Print number of rows in data frame (tibble) object
nrow(df)

## [1] 650

# Print top 6 rows of data frame (tibble) object
head(df)

## # A tibble: 6 × 7
##   EmployeeID RC_1m RC_3m RC_6m RC_9m ProPers_d1 JobPerf_12m
##   <chr>      <dbl> <dbl> <dbl> <dbl>      <dbl>       <dbl>
## 1 EE1001      13.0  18.1  31.2  42.4       50.6        47.8
## 2 EE1002      39.5  58.6  68.4  71.8       62.8        55.0
## 3 EE1003      41.3  45.6  66.4  79.3       43.8        61.7
## 4 EE1004      38.5  65.2  47.8  64.4       47.8        33.3
## 5 EE1005      34.2  37.7  57.1  72.7       64.8        46.9
## 6 EE1006      42.3  54.9  74.3  96.0      100          71.0

The data frame includes data from identical new employee onboarding surveys administered 1 month, 3 months, 6 months, and 9 months after employees’ respective start dates. The sample includes 650 employees. The data frame includes a unique identifier variable called EmployeeID, such that each employee has their own unique ID. For each survey, new employees responded to a 15-item role clarity measure using a 100-point (1 = strongly disagree and 100 = strongly agree) response format, where higher scores indicate higher role clarity. A composite variable based on employees’ average scores across the 15 items has already been created for each measurement occasion. The data frame also includes employees responses to a 10-item proactive personality measure, which was administered on their respective start dates. The proactive personality measure was also assessed using a 100-point (1 = strongly disagree and 100 = strongly agree) response format, where higher scores indicate higher proactive personality. A composite variable has already been created based on new employees’ average responses to the 10 items. Employees’ direct supervisors rated their job performance along eight dimensions at 12 months after their respective start dates using a 100-point (1 = does not meet expectations and 100 = exceeds expectations) response format. A composite variable has already been created based on new supervisors’ ratings on the eight performance dimensions. The three data sources have been joined/merged for you.

59.2.4 Visualizing Change

Prior to estimating a latent growth model (LGM), we will visualize the role clarity trajectories of our sample of 650 new employees. To do so, we need to begin by creating a second data frame in which the data are restructured from wide-to-long format. For more information on manipulating data from wide-to-long format, please see the chapter on that topic.

To restructure the data and to ultimately create our data visualization, we will use the functions from the tidyr, dplyr, and ggplot2 packages, so let’s begin by installing and accessing those packages (if you haven’t already).

# Install packages
install.packages("tidyr")
install.packages("dplyr")
install.packages("ggplot2")

# Access package
library(tidyr)
library(dplyr)
library(ggplot2)

We will begin by restructuring the data from wide-to-long format by doing the following.

1. Create a name for a new data frame object to which we will eventually assign a long-format data frame object; here, I name the new data frame object df_long.
2. Use the <- operator to assign the new long-form data frame object to the object named df_long in the step above.
3. Type the name of the original data frame object (df), followed by the pipe (%>%) operator.
4. Type the name of the pivot_longer function from the tidyr package.

1. As the first argument in the pivot_longer function, type cols= followed by the c (combine) function. As the arguments within the c function, list the names of the variables that you wish to pivot from separate variables (wide) to levels or categories of a new variable, effectively stacking them vertically. In this example, let’s list the names of role clarity variables from the four measurement occasions: RC_1m, RC_3m, RC_6m, and RC_9m.
2. As the second argument in the pivot_longer function, type names_to= followed by what you would like to name the new stacked variable (see previous) created from the four survey measure variables. Let’s call the new variable containing the names of the role clarity variables from the four measurement occasions as follows: “Time”.
3. As the third argument in the pivot_longer function, type values_to= followed by what you would like to name the new variable that contains the scores for the four role clarity variables that are now stacked vertically for each case. Let’s call the new variable containing the scores from the four variables the following: “RoleClarity”.

# Apply pivot_longer function to restructure data to long format (using pipe)
df_long <- df %>% 
  pivot_longer(cols=c(RC_1m, RC_3m, RC_6m, RC_9m),
               names_to="Time",
               values_to="RoleClarity")

# Print first 8 rows of new data frame
head(df_long, n=8)

## # A tibble: 8 × 5
##   EmployeeID ProPers_d1 JobPerf_12m Time  RoleClarity
##   <chr>           <dbl>       <dbl> <chr>       <dbl>
## 1 EE1001           50.6        47.8 RC_1m        13.0
## 2 EE1001           50.6        47.8 RC_3m        18.1
## 3 EE1001           50.6        47.8 RC_6m        31.2
## 4 EE1001           50.6        47.8 RC_9m        42.4
## 5 EE1002           62.8        55.0 RC_1m        39.5
## 6 EE1002           62.8        55.0 RC_3m        58.6
## 7 EE1002           62.8        55.0 RC_6m        68.4
## 8 EE1002           62.8        55.0 RC_9m        71.8

Using the long-format df_long data frame object as input, we will create a line chart, where each line represents an individual employee’s change in role clarity from 1 months to 9 months. We will create the line chart by doing the following operations.

1. Type the name of the long-format data frame object (df_long), followed by the pipe (%>%) operator.
2. To recode the Time variable from character to numeric, type the name of the mutate function from the dplyr package.

1. As the sole parenthetical argument, begin by typing the name of the existing Time variable followed by = so that we can overwrite the existing variable.
2. Type the name of the case_match function from the dplyr package. As the first argument, type the name of the Time variable we wish to recode. As the second argument, type the name of the first character level for the Time variable in quotation marks followed by the ~ operator and the numeral 1, which will signify one month ("RC_1m" ~ 1). As the third argument, type the name of the second character level for the Time variable in quotation marks followed by the ~ operator and the numeral 3, which will signify one month ("RC_3m" ~ 3). As the fourth argument, type the name of the third character level for the Time variable in quotation marks followed by the ~ operator and the numeral 6, which will signify one month ("RC_6m" ~ 6). As the fifth argument, type the name of the fourth character level for the Time variable in quotation marks followed by the ~ operator and the numeral 9, which will signify one month ("RC_9m" ~ 9).
3. After the last parenthesis ()) of the case_match function, insert the pipe (%>%) operator.

3. To declare the aesthetics for the plot, type the name of the ggplot function from the ggplot2 package.

1. As the sole argument in the ggplot function, type the name of the aes function. As the first argument within the aes function, type x= followed by the name of the x-axis variable, which is Time in this example. As the second argument, type y= followed by the name of the y-axis variable, which is RoleClarity in this example. As the third and final argument, type group= followed by the name of the grouping variable, which is the unique identifier variable for employees called EmployeeID (given that each employee now has four rows of data in the long-format data frame object).
2. After the ending parenthesis ()) of the ggplot function, type the + operator.

3. To request a line chart, type the name of the geom_line function.

1. We will leave the geom_line function parentheses empty.
2. After the ending parenthesis ()) of the geom_line function, type the + operator.

4. To add/change axis labels, type the name of the labs function.

1. As the first argument in the labs function, type x= followed by what we would like to label the x-axis. Let’s label the x-axis “Time”.
2. As the second argument in the labs function, type y= followed by what we would like to label the y-axis. Let’s label the y-axis “Role Clarity”.
3. After the ending parenthesis ()) of the labs function, type the + operator.

5. To change the scaling of the x-axis to reflect the unequal interval for 1 month (1) and 3 months (3) as compared to the adjacent intervals for 3 months (3) and 6 months (6) and for 6 months (6) and 9 months (9), type the name of the scale_x_continuous function.

1. As the first argument within the scale_x_continuous function, type breaks= followed by where the x-axis labels should appear along the axis, which for this example will correspond to months 1, 3, 6, and 9. We’ll use the c function to create a vector of those breaks: breaks=c(1, 3, 6, 9).
2. As the second argument, type labels= followed by the c function. Within the c function parentheses, create a vector of four descriptive names for the measurement occasions. In this example, I chose: “1 month”, “3 months”, “6 months”, and “9 months”: labels=c("1 month", "3 months", "6 months", "9 months").
3. After the ending parenthesis ()) of the scale_x_discrete function, type the + operator.

6. Type the name of the theme_classic function, and leave the function parentheses empty. This will apply a simple theme to the line chart, which includes removing background gridlines.

# Create a line chart representing employees' change trajectories
df_long %>% 
  # Recode the Time character levels to numeric values
  mutate(Time = case_match(Time,
                           "RC_1m" ~ 1,
                           "RC_3m" ~ 3,
                           "RC_6m" ~ 6,
                           "RC_9m" ~ 9)) %>%
  # Declare aesthetics for plot
  ggplot(aes(x=Time, 
             y=RoleClarity, 
             group=EmployeeID)) +
  # Create line chart
  geom_line() +
  # Create x- and y-axis labels
  labs(x="Time", 
       y="Role Clarity") + 
  # Specify the breaks and labels for the x-axis
  scale_x_continuous(breaks=c(1, 
                              3, 
                              6, 
                              9),
                     labels=c("1 month", 
                              "3 months", 
                              "6 months", 
                              "9 months")) + 
  # Request classic, minimal look without gridlines
  theme_classic()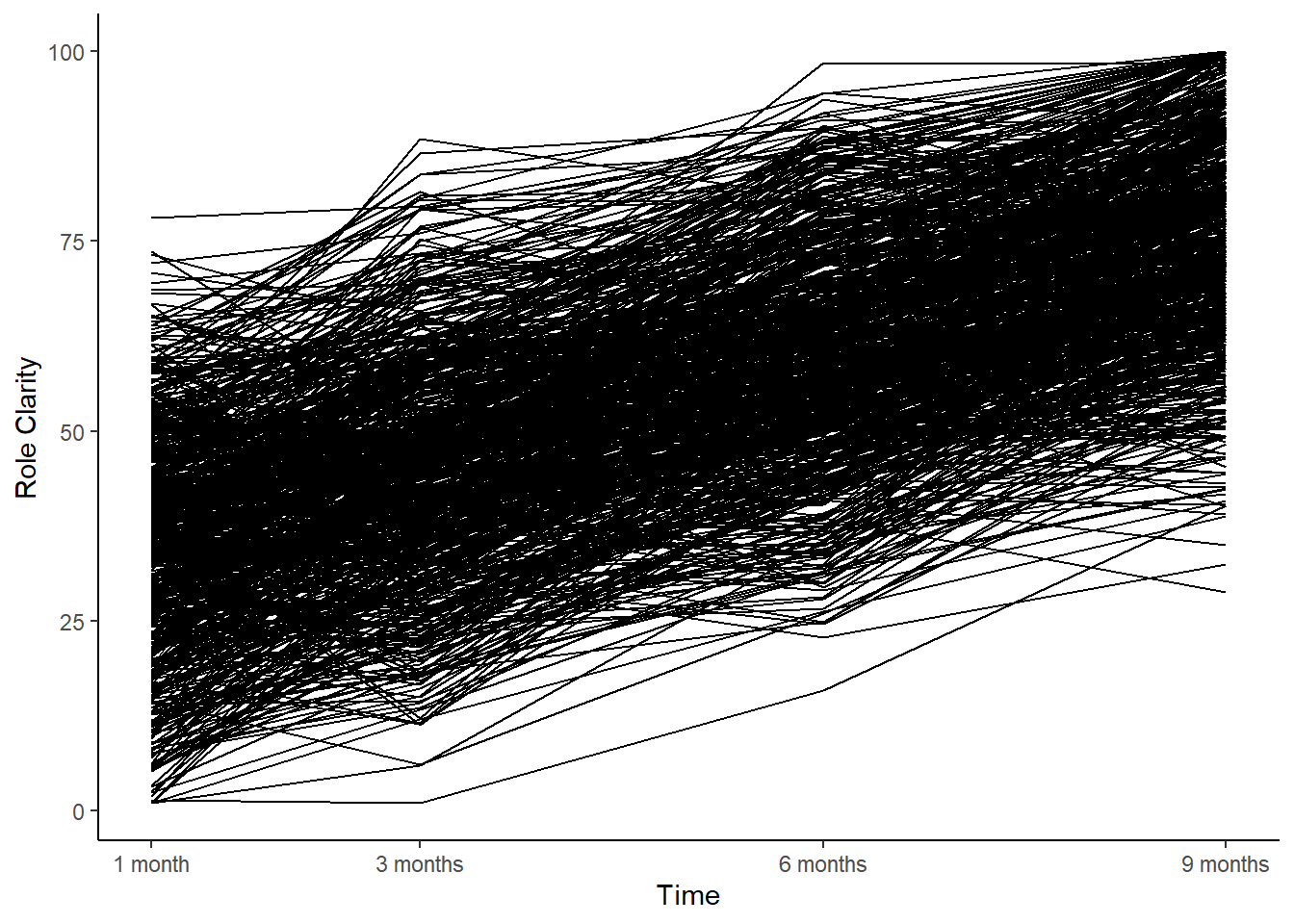

In the line chart, take note of the general upward linear trend across the 650 employees; visually, it seems clear that there is likely a linear functional form and that, on average, employees’ levels of role clarity tended to increase from 1 month to 9 months.

To view a reduced set of employees, which may give us clearer depiction of between-employee variation, we will use the slice function from the dplyr package. We will adapt the previous data visualization code by inserting the slice function after piping in the df_long data frame object. Because each employee has four rows of data in the long-format df_long data frame object, retaining the first 400 rows will represent 100 employees’ role clarity data. As the sole parenthetical argument in the slice function, let’s reference the first 400 rows of data by typing 1:400.

# Create a line chart representing a *subset* of employees' change trajectories
df_long %>% 
  # Recode the Time character levels to numeric values
  mutate(Time = case_match(Time,
                           "RC_1m" ~ 1,
                           "RC_3m" ~ 3,
                           "RC_6m" ~ 6,
                           "RC_9m" ~ 9)) %>%
  # Retain just the first 400 rows of data
  slice(1:400) %>% 
  # Declare aesthetics for plot
  ggplot(aes(x=Time, 
             y=RoleClarity, 
             group=EmployeeID)) +
  # Create line chart
  geom_line() +
  # Create x- and y-axis labels
  labs(x="Time", 
       y="Role Clarity") + 
  # Specify the breaks and labels for the x-axis
  scale_x_continuous(breaks=c(1, 
                              3, 
                              6, 
                              9),
                     labels=c("1 month", 
                              "3 months", 
                              "6 months", 
                              "9 months")) + 
  # Request classic, minimal look without gridlines
  theme_classic()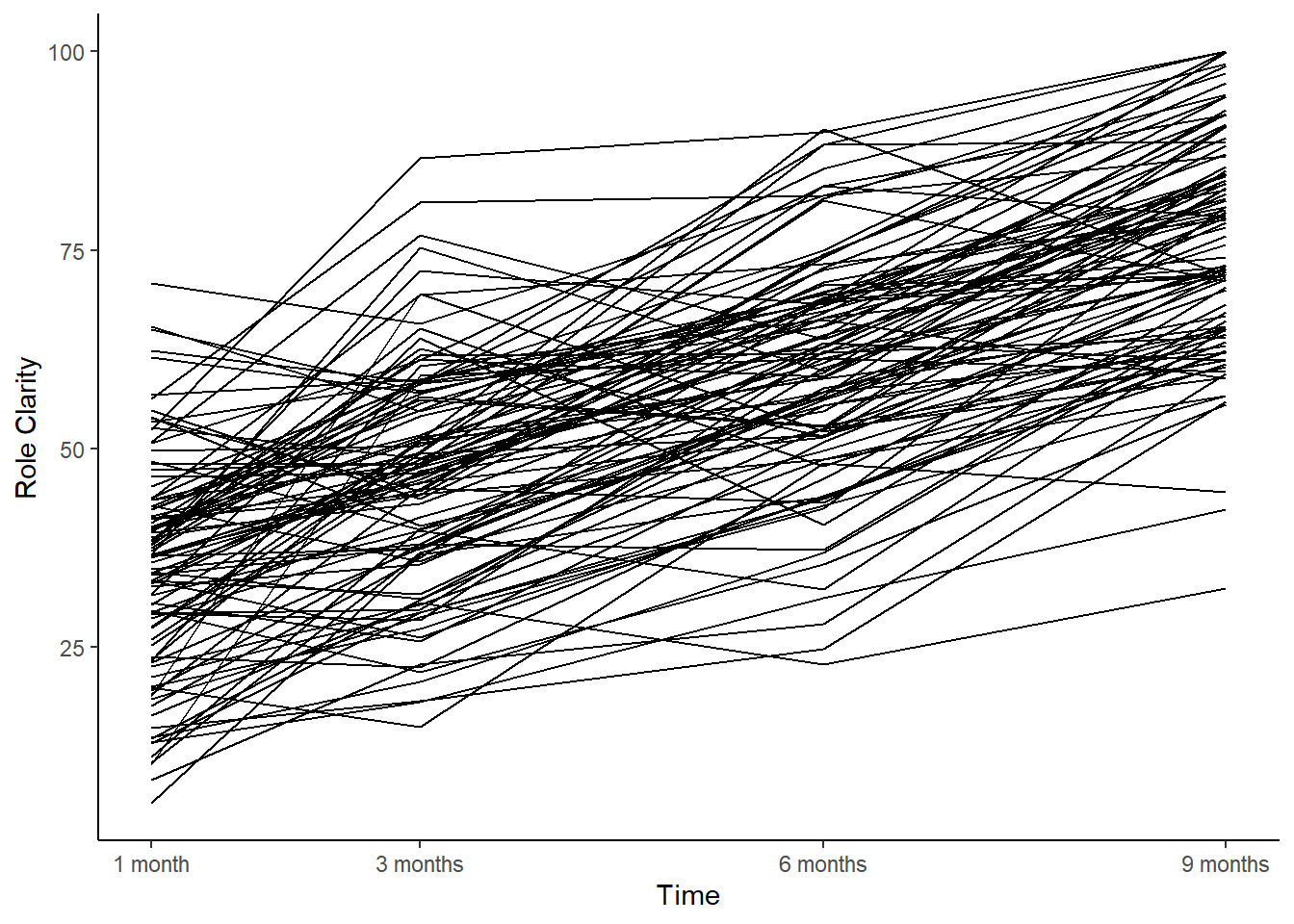

The “thinned out” line chart better captures the between-employee variation in role clarity trajectories but still suggests a positive linear function form.

59.2.5 Estimate Unconditional Unconstrained Latent Growth Model

We will begin by estimating what is referred to as an unconditional unconstrained latent growth model (LGM). An unconditional model is not conditional on an exogenous variable or variables (e.g., predictor variables, covariates). In other words, an unconditional model just includes the intercept and slope latent factors along with their respective indicators (i.e., observed repeated-measures variables). An unconstrained model lacks any constraints placed on intercept and slope means and variances and on (residual) error variances. With so many freely estimated parameters, unconstrained models tend to be the best fitting models. Finally, please note that we will be working with our data frame object that is in the original wide format: df.

Because LGM is a specific application of structural equation modeling (SEM), we will use functions from an R package developed for SEM called lavaan (latent variable analysis) to estimate our CFA models. Let’s begin by installing and accessing the lavaan package (if you haven’t already).

# Install package
install.packages("lavaan")

# Access package
library(lavaan)

First, we must specify the LGM and assign it to an object that we can subsequently reference. To do so, we will do the following.

1. Specify a name for the model object (e.g., lgm_mod), followed by the <- assignment operator.
2. To the right of the <- assignment operator and within quotation marks (" "):
3. Specify a name for the intercept latent factor (e.g., i_RC), followed by the =~ operator, which is used to indicate how a latent factor is measured. Anything that comes to the right of the =~ operator is an observed variable (i.e., indicator) of the latent factor. Please note that the latent factor is not something that we directly observe, so it will not have a corresponding variable in our data frame object.

1. After the =~ operator, specify each observed variable associated with the intercept latent factor, and to separate the observed variables, insert the + operator. In this example, the four observed variables are: RC_1m, RC_3m, RC_6m, and RC_9m. These are our observed variables, which conceptually are influenced by the underlying latent factor.
2. To set the i_RC latent factor as the intercept, we also need to constrain each observed variable’s factor loading to 1 by preceding each observed variable by 1*. As a result, the end result should look like this: i_RC =~ 1*RC_1m + 1*RC_3m + 1*RC_6m + 1*RC_9m.

4. Specify a name for the slope latent factor (e.g., s_RC), followed by the =~ operator, which is used to indicate how a latent factor is measured.

1. After the =~ operator, specify each observed variable associated with the slope latent factor, which will be the same observed variables that serve as indicators for the intercept latent factor. To separate the observed variables, insert the + operator.
2. To set the s_RC latent factor as the slope, we also need to constrain each observed variable’s factor loading to account for the time intervals between measurement occasions, which is also known as time coding. Because role clarity was measured at 1 month, 3 months, 6 months, and 9 months, we will subtract 1 from each month, which will result in the 1-month measurement occasion becoming 0 and thus setting a measurement occasion to serve as the intercept value; in other words, conceptually, the measurement occasion coded as 0 represents the value of role clarity when its slope crosses time equal to 0. Subtracting 1 from each measurement occasion in this example also allows for us to account for the unequal time intervals associated with the measurement occasions. As a result, the end result should look like this: s_RC =~ 0*RC_1m + 2*RC_3m + 5*RC_6m + 8*RC_9m.
3. Note: We could have specified a different measurement occasion slope factor loading as 0 by simply changing the time coding; for example, if we were to set the last measurement occasion slope factor loading as 0, our time coding would be: s_RC =~ -8*RC_1m + -6*RC_3m + -3*RC_6m + 0*RC_9m. Finally, if the time intervals between measurement occasions had been equal, we would have been able to apply a 0, 1, 2, and 3 time coding for the slope factor loadings to set the intercept at the first measurement occasion, or -3, -2, -1, and 0 to set the intercept at the last measurement occasion.

# Specify unconditional unconstrained LGM & assign to object
lgm_mod <- "
# Specify and constrain intercept factor loadings
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m

# Specify and constrain slope factor loadings
s_RC =~ 0*RC_1m  + 2*RC_3m  + 5*RC_6m  + 8*RC_9m
"

Second, now that we have specified the model object (lgm_mod), we are ready to estimate the model using the growth function from the lavaan package. To do so, we will do the following.

1. Specify a name for the fitted model object (e.g., lgm_fit), followed by the <- assignment operator.
2. To the right of the <- assignment operator, type the name of the growth function, and within the function parentheses include the following arguments.

1. As the first argument, insert the name of the model object that we specified above (lgm_mod).
2. As the second argument, insert the name of the data frame object to which the indicator variables in our model belong. That is, after data=, insert the name of the original wide-format data frame object (df).
3. Note: The growth function includes model estimation defaults, which explains why we had relatively few model specifications.

# Estimate unconditional unconstrained LGM & assign to fitted model object
lgm_fit  <- growth(lgm_mod,   # name of specified model object
                   data=df)   # name of wide-format data frame object

Third, we will use the summary function from base R to to print the model results. To do so, we will apply the following arguments in the summary function parentheses.

1. As the first argument, specify the name of the fitted model object that we created above (lgm_fit).
2. As the second argument, set fit.measures=TRUE to obtain the model fit indices (e.g., CFI, TLI, RMSEA, SRMR).
3. As the third argument, set standardized=TRUE to request the standardized parameter estimates for the model.

# Print summary of model results
summary(lgm_fit,             # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE)   # request standardized estimates

## lavaan 0.6.15 ended normally after 96 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         9
## 
##   Number of observations                           650
## 
## Model Test User Model:
##                                                       
##   Test statistic                                 3.760
##   Degrees of freedom                                 5
##   P-value (Chi-square)                           0.584
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1226.041
##   Degrees of freedom                                 6
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    1.000
##   Tucker-Lewis Index (TLI)                       1.001
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -10100.582
##   Loglikelihood unrestricted model (H1)     -10098.702
##                                                       
##   Akaike (AIC)                               20219.165
##   Bayesian (BIC)                             20259.458
##   Sample-size adjusted Bayesian (SABIC)      20230.883
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.000
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.047
##   P-value H_0: RMSEA <= 0.050                    0.963
##   P-value H_0: RMSEA >= 0.080                    0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.019
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                              12.463    0.820
##     RC_3m             1.000                              12.463    0.834
##     RC_6m             1.000                              12.463    0.840
##     RC_9m             1.000                              12.463    0.855
##   s_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             2.000                               1.725    0.116
##     RC_6m             5.000                               4.314    0.291
##     RC_9m             8.000                               6.902    0.474
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC             -3.483    1.147   -3.036    0.002   -0.324   -0.324
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
##     i_RC             35.143    0.559   62.824    0.000    2.820    2.820
##     s_RC              4.975    0.064   77.667    0.000    5.767    5.767
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m            75.459    7.345   10.273    0.000   75.459    0.327
##    .RC_3m            78.779    5.811   13.557    0.000   78.779    0.353
##    .RC_6m            81.083    5.791   14.001    0.000   81.083    0.368
##    .RC_9m            65.214    7.998    8.154    0.000   65.214    0.307
##     i_RC            155.324   11.703   13.273    0.000    1.000    1.000
##     s_RC              0.744    0.211    3.520    0.000    1.000    1.000

Evaluating model fit. Now that we have the summary of our model results, we will begin by evaluating key pieces of the model fit information provided in the output.

• Estimator. The function defaulted to using the maximum likelihood (ML) model estimator. When there are deviations from multivariate normality or categorical variables, the function may switch to another estimator; alternatively, we can manually switch to another estimator using the estimator= argument in the growth function.
• Number of parameters. Nine parameters were estimated, which, as we will see later, correspond to the covariance between latent factors, latent factor means, latent factor variances, and (residual) error term variances of the observed variables (i.e., indicators).
• Number of observations. Our effective sample size is 650. Had there been missing data on the observed variables, this portion of the output would have indicated how many of the observations were retained for the analysis given the missing data. How missing data are handled during estimation will depend on the type of missing data approach we apply, which is covered in more default in the section called Estimating Models with Missing Data. By default, the growth function applies listwise deletion in the presence of missing data.
• Chi-square test. The chi-square (\(\chi^{2}\)) test assesses whether the model fits the data adequately, where a statistically significant \(\chi^{2}\) value (e.g., p \(<\) .05) indicates that the model does not fit the data well and a nonsignificant chi-square value (e.g., p \(\ge\) .05) indicates that the model fits the data reasonably well. The null hypothesis for the \(\chi^{2}\) test is that the model fits the data perfectly, and thus failing to reject the null model provides some confidence that the model fits the data reasonably close to perfectly. Of note, the \(\chi^{2}\) test is sensitive to sample size and non-normal variable distributions. For this model, we find the \(\chi^{2}\) test in the output section labeled Model Test User Model. Because the p-value is equal to or greater than .05, we fail to reject the null hypothesis that the mode fits the data perfectly and thus conclude that the model fits the data acceptably (\(\chi^{2}\) = 3.760, df = 5, p = .584). Finally, note that because the model’s degrees of freedom (i.e., 5) is greater than zero, we can conclude that the model is over-identified.
• Comparative fit index (CFI). As the name implies, the comparative fit index (CFI) is a type of comparative (or incremental) fit index, which means that CFI compares our estimated model to a baseline model, which is commonly referred to as the null or independence model. CFI is generally less sensitive to sample size than the chi-square (\(\chi^{2}\)) test. A CFI value greater than or equal to .95 generally indicates good model fit to the data, although some might relax that cutoff to .90. For this model, CFI is equal to 1.000, which indicates that the model fits the data acceptably.
• Tucker-Lewis index (TLI). Like CFI, Tucker-Lewis index (TLI) is another type of comparative (or incremental) fit index. TLI is generally less sensitive to sample size than the chi-square test and tends to work well with smaller sample sizes; however, TLI may be not be the best choice for smaller sample sizes (e.g., N \(<\) 250). A TLI value greater than or equal to .95 generally indicates good model fit to the data, although like CFI, some might relax that cutoff to .90. For this model, TLI is equal to 1.001, which indicates that the model fits the data acceptably.
• Loglikelihood and Information Criteria. The section labeled Loglikelihood and Information Criteria contains model fit indices that are not directly interpretable on their own (e.g., loglikelihood, AIC, BIC). Rather, they become more relevant when we wish to compare the fit of two or more non-nested models. Given that, we will will ignore this section in this tutorial.
• Root mean square error of approximation (RMSEA). The root mean square error of approximation (RMSEA) is an absolute fit index that penalizes model complexity (e.g., models with a larger number of estimated parameters) and thus effectively rewards models that are more parsimonious. RMSEA values tend to upwardly biased when the model degrees of freedom are fewer (i.e., when the model is closer to being just-identified); further, RMSEA may not be the best choice for smaller sample sizes (e.g., N \(<\) 250). In general, an RMSEA value that is less than or equal to .06 indicates good model fit to the data, although some relax that cutoff to .08 or even .10. For this model, RMSEA is .000, which indicates that the model fits the data acceptably.
• Standardized root mean square residual. Like the RMSEA, the standardized root mean square residual (SRMR) is an example of an absolute fit index. An SRMR value that is less than or equal to .06 generally indicates good fit to the data, although some relax that cutoff to .08. For this model, SRMR is equal to .019, which indicates that the model fits the data acceptably.

In sum, the chi-square (\(\chi^{2}\)) test, CFI, TLI, RMSEA, and SRMR model fit indices all indicate that our model fit the data acceptably based on conventional rules of thumb and thresholds. This level of agreement, however, is not always going to occur. For instance, it is relatively common for the \(\chi^{2}\) test to indicate a lack of acceptable fit while one or more of the relative or absolute fit indices indicates that fit is acceptable given the limitations of the \(\chi^{2}\) test. Further, there may be instances where only two or three out of five of these model fit indices indicate acceptable model fit. In such instances, we should not necessarily toss out the model entirely, but we should consider whether there are model misspecifications. Of course, if all five model indices are well beyond the conventional thresholds (in a bad way), then our model may have some major misspecification issues, and we should proceed thoughtfully when interpreting the parameter estimates. With all that said, with an LGM, the lack of model fit indicates that there is a large amount of residual error around estimated slopes, and importantly, a lack of model fit does not necessarily indicate that there is a lack of linear (or nonlinear) change. For our model, all five model fit indices signal that the model fit the data acceptably, and thus we should feel confident proceeding forward with interpreting and evaluating the parameter estimates.

Evaluating parameter estimates. As noted above, our model showed acceptable fit to the data, so we can feel comfortable interpreting the parameter estimates. By default, the growth function provides unstandardized parameter estimates, but if you recall, we also requested standardized parameter estimates. In the output, the unstandardized parameter estimates fall under the column titled Estimates, whereas the standardized factor loadings we’re interested in fall under the column titled Std.all.

• Factor loadings. The output section labeled Latent Variables contains our factor loadings for the intercept and slope latent factors.
  • With respect to the unstandardized factor loadings for the intercept latent factor (i_RC; see Estimates column), the constraints we applied are reported. Specifically, we constrained each of the intercept factor loadings to 1.
  • With respect to the unstandardized factor loadings for the slope latent factor (s_RC; see Estimates column), the constraints we applied are reported. Specifically, we constrained slope factor loadings to 0, 2, 5, and 8 to correspond with measurement occasions 1 month, 3 months, 6 months, and 9 months.
• Covariances. The output section labeled Covariances contains the covariance between the intercept and slope latent factors. The unstandardized estimate is -3.483 (p = .002), and the standardized estimate, which can be interpreted as a correlation, is -.324.
• Means & Intercepts. The output section labeled Intercepts contains the means for the latent factors and the intercepts for the observed variables. By default, the intercepts for the observed variables are constrained to zero, so those are not of substantive interest. The means for the intercept and slope latent factors are, however, of substantive interest. The unstandardized intercept latent factor mean of 35.143 (p < .001) indicates that, on average, new employees’ level of role clarity was 35.143 (out of a possible 100) 1 month after their respective start dates. The unstandardized slope latent factor mean of 4.975 (p < .001) indicates that, on average, new employees’ level of role clarity increased by 4.975 each month.
• Variances. The output section labeled Variances contains the (residual) error variances for each observed variable (i.e., indicator) of the latent factors and the variances of the latent factors. The unstandardized variance associated with the intercept latent factor indicates that there is a statistically significant amount of between-employee intercept variation (155.324, p < .001), and the unstandardized variance associated with the slope latent factor indicates that there is a statistically significant amount of between-employee slope variation (.744, p < .001). The standardized (residual) error variances associated with the four observed role clarity measurement occasions ranged from .307 to .368, indicating that a proportionally small amount of variance was left unexplained by the intercept and slope latent factors and that the error variances are similar in magnitude, potentially suggesting homogeneity of residual error variances.

Visualize the path diagram. To visualize our unconditional unconstrained LGM as a path diagram, we can use the semPaths function from the semPlot package. If you haven’t already, please install and access the semPlot package.

# Install package
install.packages("semPlot")

# Access package
library(semPlot)

While there are many arguments that can be used to refine the path diagram visualization, we will focus on just four to illustrate how the semPaths function works.

1. As the first argument, insert the name of the fitted LGM object (lgm_fit).
2. As the second argument, specify what="est" to display just the unstandardized parameter estimates.
3. As the third argument, specify weighted=FALSE to request that the visualization not weight the edges (e.g., lines) and other plot features.
4. As the fourth argument, specify nCharNodes=0 in order to use the full names of latent and observed indicator variables instead of abbreviating them.

# Visualize the unconditional unconstrained LGM
semPaths(lgm_fit,         # name of fitted model object 
         what="est",      # display unstandardized parameter estimates
         weighted=FALSE,  # do not weight plot features
         nCharNodes=0)    # do not abbreviate names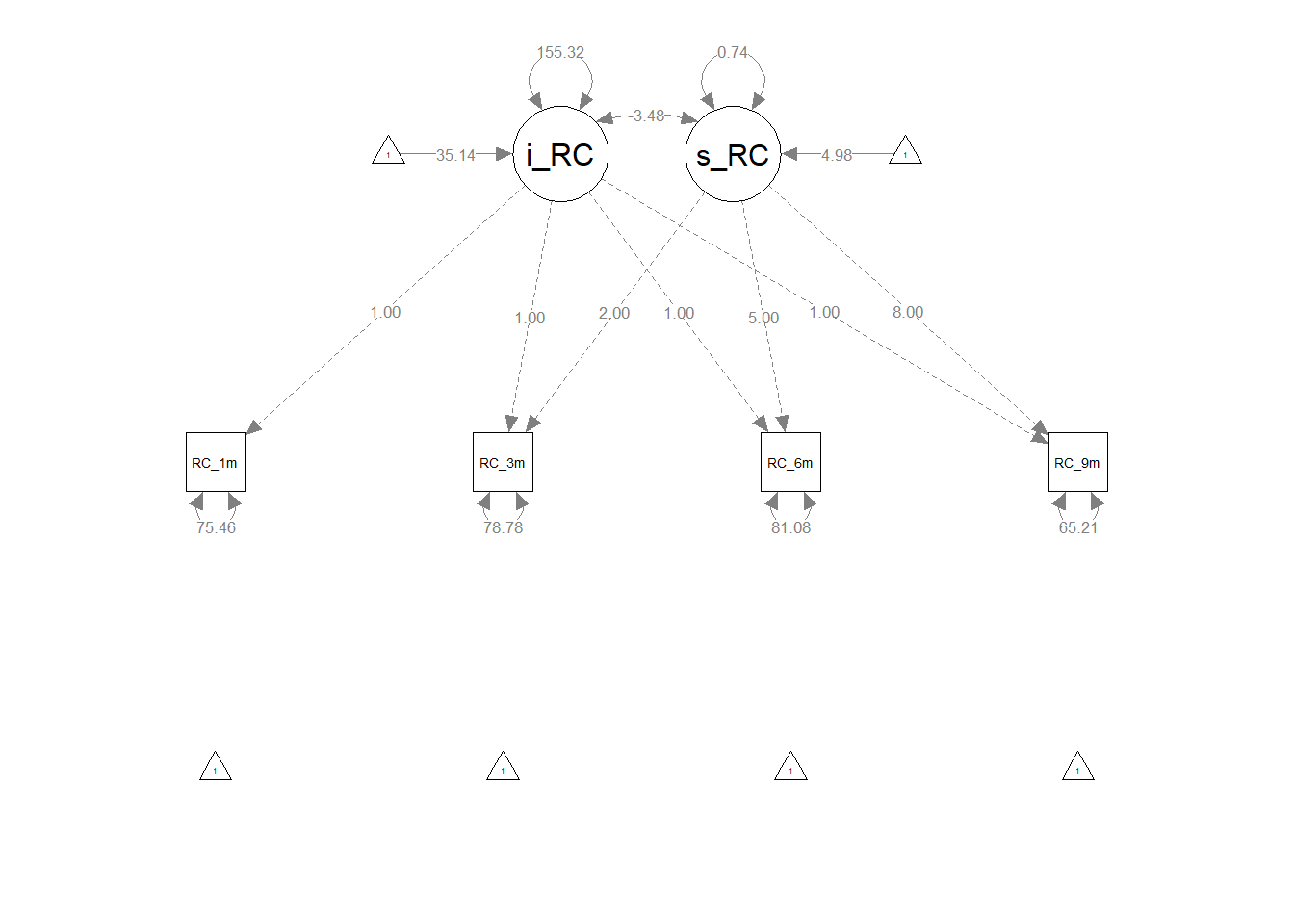

The resulting LGM path diagram can be useful for interpreting the model specifications and the parameter estimates.

Results write-up for the unconditional unconstrained LGM. As part of a new-employee onboarding longitudinal study, surveys were administered 1 month, 3 months, 6 months, and 9 months after employees’ respective start dates. Each survey included a 15-item measure of role clarity, and a composite variable based on the employees’ average responses was created at each survey measurement occasion. Using an unconditional unconstrained latent growth model (LGM), we investigated whether new employees’ levels of role clarity showed linear change over time and whether role-clarity change varied between new employees. When specifying the model, we constrained the intercept factor loadings to 1, and constrained the slope factor loadings to 0, 2, 5, and 8 to account for the unequal time intervals between adjacent measurement occasions. We estimated the model using the maximum likelihood (ML) estimator and a sample size of 650 new employees. Missing data were not a concern. We evaluated the model’s fit to the data using the chi-square (\(\chi^{2}\)) test, CFI, TLI, RMSEA, and SRMR model fit indices. The \(\chi^{2}\) test indicated that the model fit the data as well as a perfectly fitting model (\(\chi^{2}\) = 3.760 df = 5, p = .584). Further, the CFI and TLI estimates were 1.000 and 1.001, respectively, which exceeded the more stringent threshold of .95, thereby indicating that model showed acceptable fit to the data. Similarly, the RMSEA estimate was .00, which was below the more stringent threshold of .06, thereby indicating that model showed acceptable fit to the data. The SRMR estimate was .019, which was below the stringent threshold of .06, thereby indicating acceptable model fit to the data. Collectively, the model fit information indicated that model fit the data acceptably. Regarding the unstandardized parameter estimates, the intercept latent factor mean of 35.143 (p < .001) indicated that, on average, new employees’ level of role clarity was 35.143 (out of a possible 100) 1 month after their respective start dates. The slope latent factor mean of 4.975 (p < .001) indicated that, on average, new employees’ level of role clarity increased by 4.975 each month. The variances associated with the intercept and slope latent factors, however, indicated that there was a statistically significant amount of between-employee intercept and slope variation (\(\sigma_{intercept}\) = 155.324, p < .001; \(\sigma_{slope}\) = .744, p < .001). The statistically significant and negative covariance between the intercept and slope latent factors indicated that employees with higher levels of role clarity 1 month after their respective start dates tended to have less positive role clarity change trajectories (\(\psi\) = -3.483, p = .002). Finally, the standardized (residual) error terms associated with the four observed role clarity measurement occasions ranged from .307 to .368, indicating that a proportionally small amount of variance was left unexplained by the intercept and slope latent factors. In sum, the estimated unconditional constrained LGM showed that new employees’ role clarity, on average, increased in a linear manner between 1 month and 9 months after employees’ respective start dates. Further, new employees varied with respect to their level of role clarity 1 month after their start dates, and their role clarity change trajectories varied in terms of slope. A conditional model with a time-invariant predictor or time-variant predictors may help explain between-employee differences in intercepts and slopes.

59.2.6 Nested Model Comparisons

When possible, we typically prefer to arrive at a model that not only fits the data but also is parsimonious in nature (i.e., less complex). With respect to LGM, there are variety of circumstances in which we might wish to compare nested models to arrive at a well-fitting yet parsimonious model. A nested model has all the same parameter estimates of a full model but has additional parameter constraints in place; a nested model will have more degrees of freedom (df) than the full model, thereby indicating that the nested model is less complex.

In this section, we will build up to the unconditional unconstrained LGM from the previous section by gradually relaxing constraints. In general, our goal will be to retain the most parsimonious model that fits the data acceptably.

59.2.6.1 Estimate Baseline Model

We will begin with evaluating a very simple model that we’ll refer to as the baseline model. For this model, we will freely estimate the mean of the intercept latent factor, constrain the (residual) error variances to be zero, and constrain all remaining parameters from our unconditional unconstrained model (from the previous section) to be zero. In other words, we will evaluate an intercept-only model in which intercepts aren’t allowed to vary between employees and in which the residual error variances constrained (i.e., homogeneity of variances). We will directly specify all necessary model parameters (even those that would be estimated by default), as in subsequent models we will be relaxing some of the constraints we put in place in this baseline model.

1. Specify a name for the model object (e.g., lgm_mod1), followed by the <- assignment operator.
2. To the right of the <- assignment operator and within quotation marks (" "):
3. Specify a name for the intercept latent factor (e.g., i_RC), followed by the =~ operator, which is used to indicate how a latent factor is measured.

1. After the =~ operator, specify each observed variable associated with the intercept latent factor, and to separate the observed variables, insert the + operator. In this example, the four observed variables are: RC_1m, RC_3m, RC_6m, and RC_9m. These are our observed variables, which conceptually are influenced by the underlying latent factor.
2. To set the i_RC latent factor as the intercept, we also need to constrain each observed variable’s factor loading to 1 by preceding each observed variable by 1*. As a result, the end result should look like this: i_RC =~ 1*RC_1m + 1*RC_3m + 1*RC_6m + 1*RC_9m.

4. Specify a name for the slope latent factor (e.g., s_RC), followed by the =~ operator, which is used to indicate how a latent factor is measured.

1. After the =~ operator, specify each observed variable associated with the slope latent factor, which will be the same observed variables that serve as indicators for the intercept latent factor.
2. Because we will not be freely estimating the slope in this baseline model, we will constrain all s_RC latent factor loadings to zero, which will look like this: s_RC =~ 0*RC_1m + 0*RC_3m + 0*RC_6m + 0*RC_9m.

5. Freely estimate the mean of the intercept factor by specifying the name of the latent factor (i_RC) followed by the ~ operator and 1. Specifying ~ 1 after a latent factor freely estimates the mean (or intercept) of that factor.
6. Because we are setting our slope to be zero in this model, we need to constrain the mean of the slope factor to zero by specifying the name of the latent factor (s_RC) followed by the ~ operator and 0*1. Specifying s_RC ~ 0*1 constrains the mean (or intercept) of the latent factor to zero.
7. Constrain the intercept latent factor variance to zero, which means we won’t allow intercepts to vary between employees. To do so, specify the variance of the latent factor (e.g, i_RC ~~ i_RC), except insert 0* to the right of the ~~ (variance) operator to constrain the variance to zero. The end result should look like this: i_RC ~~ 0*i_RC.
8. Constrain the slope latent factor variance to zero as well. To do so, specify the following: s_RC ~~ 0*s_RC.
9. Constrain the covariance between the intercept and slope latent factors to zero by specifying the following: i_RC ~~ 0*s_RC.
10. Constrain the (residual) error variances to be equal by first specifying the variance of each observed variable (e.g., RC_1m ~~ RC_1m); however, we will apply equality constraints by inserting the same letter or word immediately after the ~~ (covariance) operator. I’ve chosen to use the letter e as the equality constraint. For example, applying the equality constraint to the first observed variable will look like this: RC_1m ~~ e*RC_1m.
11. Specify a name for the fitted model object (e.g., lgm_fit1), followed by the <- assignment operator.
12. To the right of the <- assignment operator, type the name of the growth function, and within the function parentheses include the following arguments.

1. As the first argument, insert the name of the model object that we specified above (lgm_mod1).
2. As the second argument, insert the name of the data frame object to which the indicator variables in our model belong. That is, after data=, insert the name of the original wide-format data frame object (df).
3. Note: The growth function includes model estimation defaults, which explains why we had relatively few model specifications.

13. Specify the name of the summary function from base R.

1. As the first argument, specify the name of the fitted model object that we created above (lgm_fit1).
2. As the second argument, set fit.measures=TRUE to obtain the model fit indices (e.g., CFI, TLI, RMSEA, SRMR).
3. As the third argument, set standardized=TRUE to request the standardized parameter estimates for the model.

14. Specify the name of the semPaths function.

1. As the first argument, insert the name of the fitted LGM object (lgm_fit1).
2. As the second argument, specify what="est" to display just the unstandardized parameter estimates.
3. As the third argument, specify weighted=FALSE to request that the visualization not weight the edges (e.g., lines) and other plot features.
4. As the fourth argument, specify nCharNodes=0 in order to use the full names of latent and observed indicator variables instead of abbreviating them.

# Specify baseline model & assign to object
lgm_mod1 <- "
# Specify and constrain intercept factor loadings
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m 

# Specify and constrain slope factor loadings to zero (no growth)
s_RC =~ 0*RC_1m  + 0*RC_3m  + 0*RC_6m  + 0*RC_9m

# Freely estimate mean of intercept latent factor
i_RC ~ 1

# Constrain mean of slope latent factor to zero (average slope set to zero)
s_RC ~ 0*1

# Constrain intercept latent factor variance to zero (don't allow to vary)
i_RC ~~ 0*i_RC

# Constrain slope latent factor variance to zero (don't allow to vary)
s_RC ~~ 0*s_RC

# Constrain covariance between intercept & slope latent factors to zero
i_RC ~~ 0*s_RC

# Constrain (residual) error variances to be equal (homogeneity of variances)
RC_1m ~~ e*RC_1m
RC_3m ~~ e*RC_3m
RC_6m ~~ e*RC_6m
RC_9m ~~ e*RC_9m
"

# Estimate LGM & assign to fitted model object
lgm_fit1  <- growth(lgm_mod1,  # name of specified model object
                    data=df)   # name of wide-format data frame object
                   
# Print summary of model results
summary(lgm_fit1,              # name of fitted model object
        fit.measures=TRUE,     # request model fit indices
        standardized=TRUE)     # request standardized estimates

## lavaan 0.6.15 ended normally after 17 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         5
##   Number of equality constraints                     3
## 
##   Number of observations                           650
## 
## Model Test User Model:
##                                                       
##   Test statistic                              3062.245
##   Degrees of freedom                                12
##   P-value (Chi-square)                           0.000
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1226.041
##   Degrees of freedom                                 6
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.000
##   Tucker-Lewis Index (TLI)                      -0.250
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -11629.825
##   Loglikelihood unrestricted model (H1)     -10098.702
##                                                       
##   Akaike (AIC)                               23263.649
##   Bayesian (BIC)                             23272.603
##   Sample-size adjusted Bayesian (SABIC)      23266.253
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.625
##   90 Percent confidence interval - lower         0.607
##   90 Percent confidence interval - upper         0.644
##   P-value H_0: RMSEA <= 0.050                    0.000
##   P-value H_0: RMSEA >= 0.080                    1.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.877
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                               0.000    0.000
##     RC_3m             1.000                               0.000    0.000
##     RC_6m             1.000                               0.000    0.000
##     RC_9m             1.000                               0.000    0.000
##   s_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             0.000                               0.000    0.000
##     RC_6m             0.000                               0.000    0.000
##     RC_9m             0.000                               0.000    0.000
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC              0.000                                 NaN      NaN
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC             53.805    0.416  129.403    0.000      Inf      Inf
##     s_RC              0.000                                 NaN      NaN
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC              0.000                                 NaN      NaN
##     s_RC              0.000                                 NaN      NaN
##    .RC_1m      (e)  449.503   12.467   36.056    0.000  449.503    1.000
##    .RC_3m      (e)  449.503   12.467   36.056    0.000  449.503    1.000
##    .RC_6m      (e)  449.503   12.467   36.056    0.000  449.503    1.000
##    .RC_9m      (e)  449.503   12.467   36.056    0.000  449.503    1.000

# Visualize the LGM as a path diagram
semPaths(lgm_fit1,             # name of fitted model object 
         what="est",           # display unstandardized parameter estimates
         weighted=FALSE,       # do not weight plot features
         nCharNodes=0)         # do not abbreviate names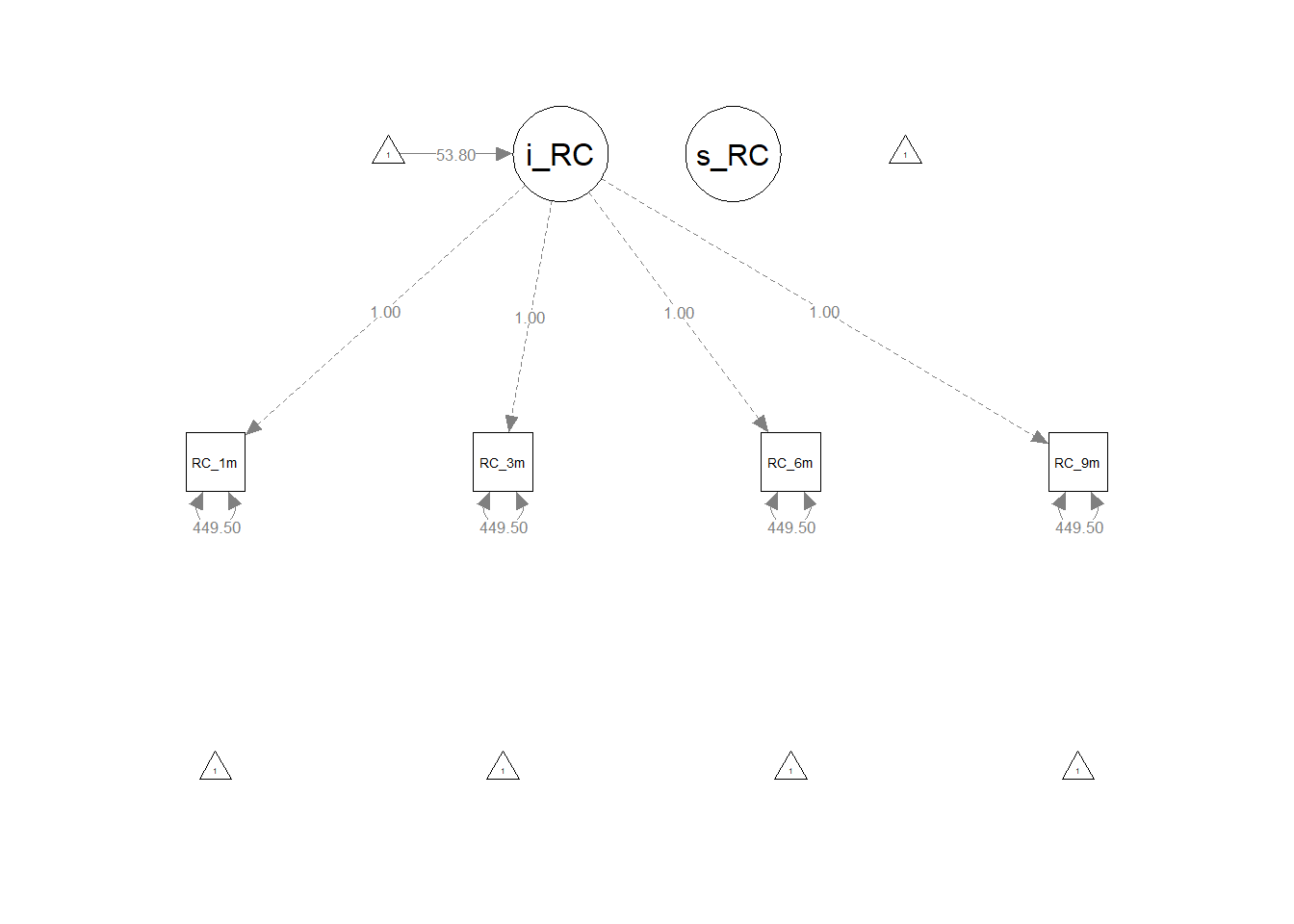

Like we did with the unconditional unconstrained model in the previous section, we typically begin by evaluating the model fit, and if the model fit appears acceptable, then we go on to evaluate the parameter estimates. To save space, however, we will just summarize the baseline model fit indices in the table below.

Model	\(\chi^{2}\)	df	p	CFI	TLI	RMSEA	SRMR
Baseline Model	3062.245	12	< .001	.000	-2.500	.625	.877

As you can see above, the baseline model fits the data very poorly, which means that relaxing some of the constraints should improve the model’s fit to the data.

59.2.6.2 Freely Estimate Variance of Intercept Latent Factor

We will treat the baseline model as our nested model, and in this section, we will compare the baseline model to a more complex model (i.e., more freely estimated parameters). Specifically, we will specify a model in which we freely estimate the variance of the intercept latent factor. We’ll begin with the same model specifications as the baseline model, except we will relax the constraint on the variance of the intercept latent factor (i_RC) in order to freely estimate it. As indicated by the model specification annotation with three hashtags (###) instead of the typical one hashtag, we will freely estimate the variance of the intercept latent factor by removing 0*, such that the resulting line is now: i_RC ~~ i_RC. Beyond that, we will change the model specification object name to lgm_mod2 and the fitted model object to lgm_fit2 for subsequent model comparison purposes.

# Specify freely estimated intercept factor variance & assign to object
lgm_mod2 <- "
# Specify and constrain intercept factor loadings
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m 

# Specify and constrain slope factor loadings to zero (no growth)
s_RC =~ 0*RC_1m  + 0*RC_3m  + 0*RC_6m  + 0*RC_9m

# Freely estimate mean of intercept latent factor
i_RC ~ 1

# Constrain mean of slope latent factor to zero (average slope set to zero)
s_RC ~ 0*1

### Freely estimate intercept latent factor variance (allow to vary)
i_RC ~~ i_RC

# Constrain slope latent factor variance to zero (don't allow to vary)
s_RC ~~ 0*s_RC

# Constrain covariance between intercept & slope latent factors to zero
i_RC ~~ 0*s_RC

# Constrain (residual) error variances to be equal (homogeneity of variances)
RC_1m ~~ e*RC_1m
RC_3m ~~ e*RC_3m
RC_6m ~~ e*RC_6m
RC_9m ~~ e*RC_9m
"

# Estimate LGM & assign to fitted model object
lgm_fit2  <- growth(lgm_mod2,  # name of specified model object
                    data=df)   # name of wide-format data frame object
                   
# Print summary of model results
summary(lgm_fit2,              # name of fitted model object
        fit.measures=TRUE,     # request model fit indices
        standardized=TRUE)     # request standardized estimates

## lavaan 0.6.15 ended normally after 21 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         6
##   Number of equality constraints                     3
## 
##   Number of observations                           650
## 
## Model Test User Model:
##                                                       
##   Test statistic                              2997.931
##   Degrees of freedom                                11
##   P-value (Chi-square)                           0.000
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1226.041
##   Degrees of freedom                                 6
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.000
##   Tucker-Lewis Index (TLI)                      -0.335
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -11597.668
##   Loglikelihood unrestricted model (H1)     -10098.702
##                                                       
##   Akaike (AIC)                               23201.336
##   Bayesian (BIC)                             23214.767
##   Sample-size adjusted Bayesian (SABIC)      23205.242
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.646
##   90 Percent confidence interval - lower         0.627
##   90 Percent confidence interval - upper         0.666
##   P-value H_0: RMSEA <= 0.050                    0.000
##   P-value H_0: RMSEA >= 0.080                    1.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.809
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                               7.873    0.371
##     RC_3m             1.000                               7.873    0.371
##     RC_6m             1.000                               7.873    0.371
##     RC_9m             1.000                               7.873    0.371
##   s_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             0.000                               0.000    0.000
##     RC_6m             0.000                               0.000    0.000
##     RC_9m             0.000                               0.000    0.000
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC              0.000                                 NaN      NaN
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC             53.805    0.494  108.834    0.000    6.834    6.834
##     s_RC              0.000                                 NaN      NaN
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC             61.987    9.343    6.635    0.000    1.000    1.000
##     s_RC              0.000                                 NaN      NaN
##    .RC_1m      (e)  387.516   12.410   31.225    0.000  387.516    0.862
##    .RC_3m      (e)  387.516   12.410   31.225    0.000  387.516    0.862
##    .RC_6m      (e)  387.516   12.410   31.225    0.000  387.516    0.862
##    .RC_9m      (e)  387.516   12.410   31.225    0.000  387.516    0.862

# Visualize the LGM as a path diagram
semPaths(lgm_fit2,             # name of fitted model object 
         what="est",           # display unstandardized parameter estimates
         weighted=FALSE,       # do not weight plot features
         nCharNodes=0)         # do not abbreviate names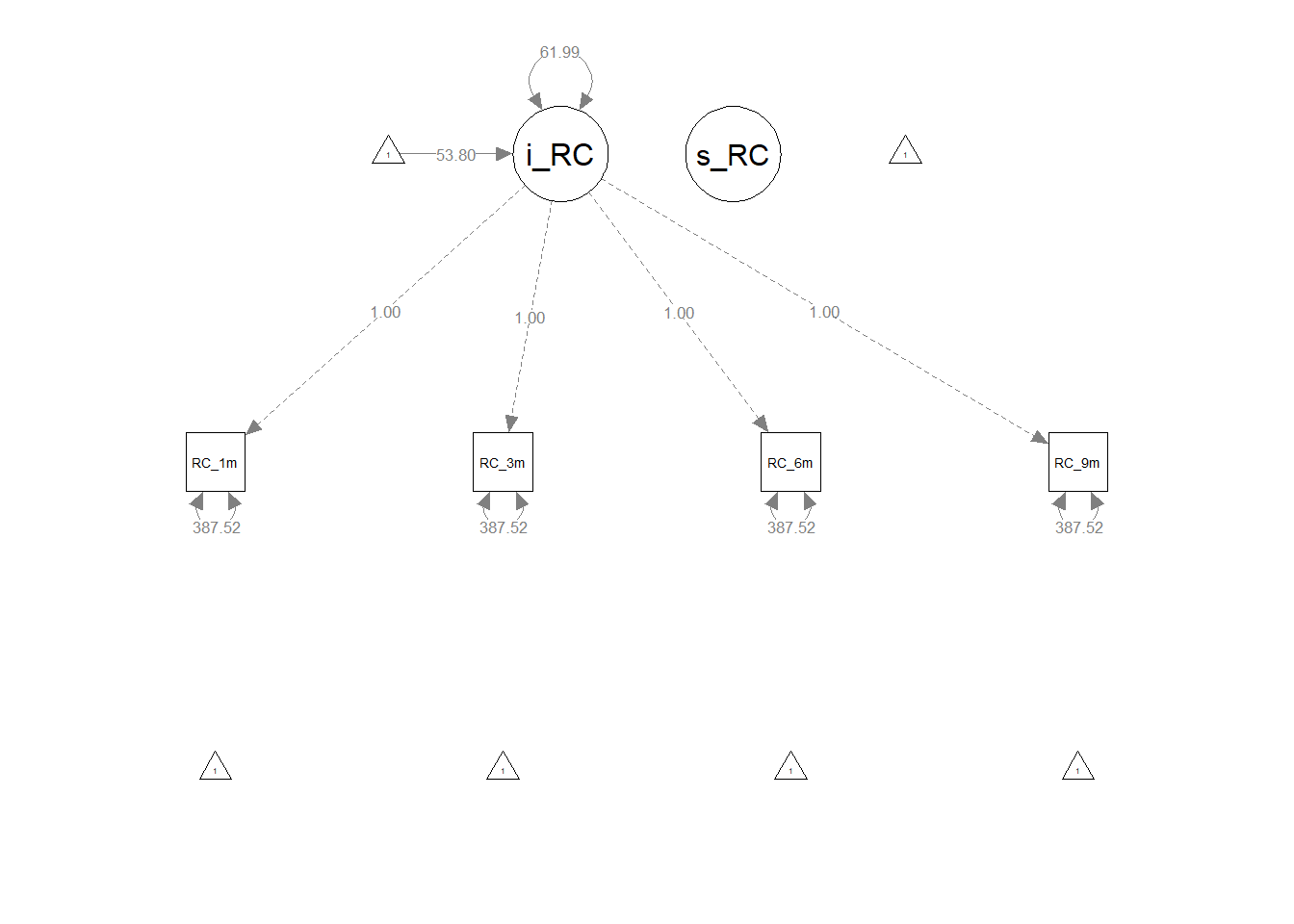

Below, I’ve expanded upon the previous table by adding in the model fit information for the freely estimated intercept latent factor variance.

Model	\(\chi^{2}\)	df	p	CFI	TLI	RMSEA	SRMR
Baseline Model	3062.245	12	< .001	.000	-2.500	.625	.877
Free Intercept Variance Model	2997.931	11	< .001	.000	-0.335	.646	.809

Both the baseline model and the new model fit the data pretty poorly.

As an additional test, we can perform a nested model comparison using the chi-square (\(\chi^{2}\)) difference test, which is also known as the log-likelihood (LL) test. To perform this test, we’ll apply the anova function from base R. As the first argument, we’ll insert the name of our model containing the freely estimated intercept latent factor variance fitted model object (lgm_fit2), and as the second argument, we’ll insert the name of our baseline fitted model object (lgm_fit1).

# Nested model comparison using chi-square difference test
anova(lgm_fit2, lgm_fit1)

## 
## Chi-Squared Difference Test
## 
##          Df   AIC   BIC  Chisq Chisq diff  RMSEA Df diff           Pr(>Chisq)    
## lgm_fit2 11 23201 23215 2997.9                                                   
## lgm_fit1 12 23264 23273 3062.2     64.314 0.3121       1 0.000000000000001061 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The chi-square difference test indicates that the baseline model fits the data statistically significantly worse than the current less parsimonious model in which we freely estimated the variance of the intercept latent factor (\(\Delta \chi^{2}\) = 64.314, \(\Delta df\) = 1, \(p\) < .001).

Note: If your anova function output defaulted to scientific notation, you can “turn off” scientific notation using the following function. After running the options function below, you can re-run the anova function to get the output in traditional notation.

# Turn off scientific notation
options(scipen=9999)

59.2.6.3 Specify Linear Functional Form for Slope Latent Factor & Estimate Its Mean

For this model, we will update our previous model by specifying the function form of the slope latent factor and freely estimating its mean. Updates to the previous model specifications are preceded with ### annotations. Specifically, we will apply meaningful time coding to the s_RC latent factor. Because role clarity was measured at 1 month, 3 months, 6 months, and 9 months, we will subtract 1 from each month, which will result in the 1-month measurement occasion becoming 0 and thus setting a measurement occasion to serve as the intercept value; in other words, conceptually, the measurement occasion coded as 0 represents the value of role clarity when its slope crosses time equal to 0. Subtracting 1 from each measurement occasion in this example also allows for us to account for the unequal time intervals associated with the measurement occasions. As a result, the end result should look like this: s_RC =~ 0*RC_1m + 2*RC_3m + 5*RC_6m + 8*RC_9m. In addition, we will relax the constraint on the mean of the slope latent factor (s_RC) in order to freely estimate it, which requires removing 0*, such that the resulting line is now: s_RC ~ 1. Beyond that, we will change the model specification object name to lgm_mod3 and the fitted model object to lgm_fit3 for subsequent model comparison purposes.

# Specify linear functional form for slope latent factor & assign to object
lgm_mod3 <- "
# Specify and constrain intercept factor loadings
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m 

### Specify and constrain slope factor loadings to linear growth
s_RC =~ 0*RC_1m  + 2*RC_3m  + 5*RC_6m  + 8*RC_9m

# Freely estimate mean of intercept latent factor
i_RC ~ 1

### Freely estimate mean of slope latent factor
s_RC ~ 1

# Freely estimate intercept latent factor variance (allow to vary)
i_RC ~~ i_RC

# Constrain slope latent factor variance to zero (don't allow to vary)
s_RC ~~ 0*s_RC

# Constrain covariance between intercept & slope latent factors to zero
i_RC ~~ 0*s_RC

# Constrain (residual) error variances to be equal (homogeneity of variances)
RC_1m ~~ e*RC_1m
RC_3m ~~ e*RC_3m
RC_6m ~~ e*RC_6m
RC_9m ~~ e*RC_9m
"

# Estimate LGM & assign to fitted model object
lgm_fit3  <- growth(lgm_mod3,  # name of specified model object
                    data=df)   # name of wide-format data frame object
                   
# Print summary of model results
summary(lgm_fit3,              # name of fitted model object
        fit.measures=TRUE,     # request model fit indices
        standardized=TRUE)     # request standardized estimates

## lavaan 0.6.15 ended normally after 25 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         7
##   Number of equality constraints                     3
## 
##   Number of observations                           650
## 
## Model Test User Model:
##                                                       
##   Test statistic                                20.422
##   Degrees of freedom                                10
##   P-value (Chi-square)                           0.026
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1226.041
##   Degrees of freedom                                 6
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.991
##   Tucker-Lewis Index (TLI)                       0.995
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -10108.913
##   Loglikelihood unrestricted model (H1)     -10098.702
##                                                       
##   Akaike (AIC)                               20225.826
##   Bayesian (BIC)                             20243.734
##   Sample-size adjusted Bayesian (SABIC)      20231.034
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.040
##   90 Percent confidence interval - lower         0.014
##   90 Percent confidence interval - upper         0.065
##   P-value H_0: RMSEA <= 0.050                    0.716
##   P-value H_0: RMSEA >= 0.080                    0.003
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.034
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                              11.740    0.788
##     RC_3m             1.000                              11.740    0.788
##     RC_6m             1.000                              11.740    0.788
##     RC_9m             1.000                              11.740    0.788
##   s_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             2.000                               0.000    0.000
##     RC_6m             5.000                               0.000    0.000
##     RC_9m             8.000                               0.000    0.000
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC              0.000                                 NaN      NaN
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC             35.144    0.542   64.820    0.000    2.994    2.994
##     s_RC              4.976    0.059   83.832    0.000      Inf      Inf
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC            137.824    8.838   15.594    0.000    1.000    1.000
##     s_RC              0.000                                 NaN      NaN
##    .RC_1m      (e)   84.169    2.696   31.225    0.000   84.169    0.379
##    .RC_3m      (e)   84.169    2.696   31.225    0.000   84.169    0.379
##    .RC_6m      (e)   84.169    2.696   31.225    0.000   84.169    0.379
##    .RC_9m      (e)   84.169    2.696   31.225    0.000   84.169    0.379

# Visualize the LGM as a path diagram
semPaths(lgm_fit3,             # name of fitted model object 
         what="est",           # display unstandardized parameter estimates
         weighted=FALSE,       # do not weight plot features
         nCharNodes=0)         # do not abbreviate names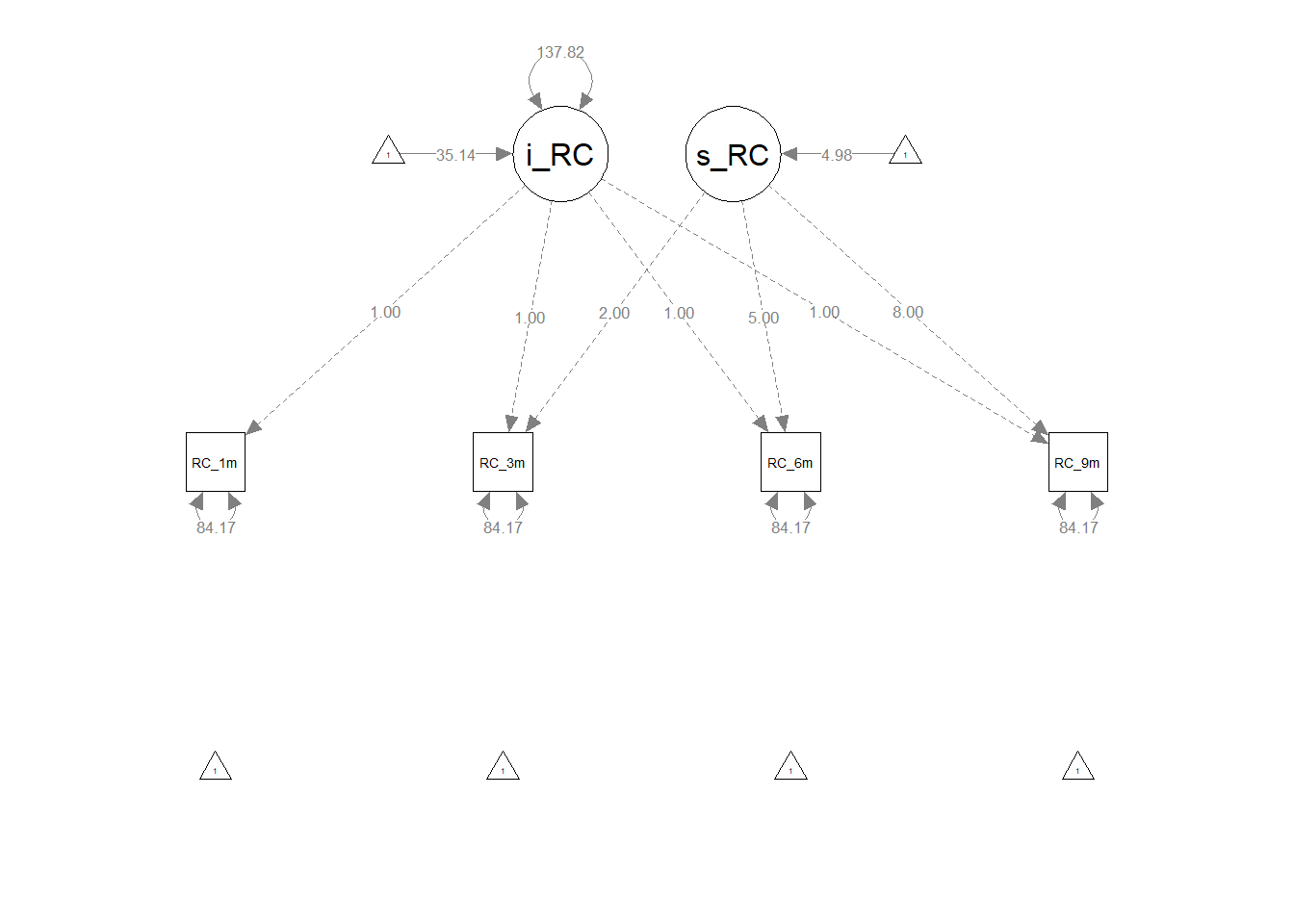

Below, I’ve expanded upon the previous model comparison table by adding in the model fit information for the model in which we specified a linear functional form for the slope latent factor and freely estimated the mean of the slope latent factor.

Model	\(\chi^{2}\)	df	p	CFI	TLI	RMSEA	SRMR
Baseline Model	3062.245	12	< .001	.000	-2.500	.625	.877
Free Intercept Variance Model	2997.931	11	< .001	.000	-0.335	.646	.809
Linear Slope Latent Factor Model	20.422	10	.026	.991	.995	.040	.034

As you can see above, our model fit indices improve considerably when we specify a linear function form for the latent slope factor and allow its mean to be freely estimated.

As before, we’ll also estimate the chi-square (\(\chi^{2}\)) difference test, except this time we’ll compare the current model (lgm_fit3) to the previous model (lgm_fit2).

# Nested model comparison using chi-square difference test
anova(lgm_fit3, lgm_fit2)

## 
## Chi-Squared Difference Test
## 
##          Df   AIC   BIC    Chisq Chisq diff  RMSEA Df diff            Pr(>Chisq)    
## lgm_fit3 10 20226 20244   20.422                                                    
## lgm_fit2 11 23201 23215 2997.931     2977.5 2.1399       1 < 0.00000000000000022 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The chi-square difference test indicates that the current model fits the data statistically significantly better than the previous model (\(\Delta \chi^{2}\) = 2977.5, \(\Delta df\) = 1, \(p\) < .001). This corroborates what we saw with the direct comparison of model fit indices above.

59.2.6.4 Freely Estimate Variance of Slope Latent Factor

For this model, we will update our previous model by allowing slopes to freely vary between employees; in other words, we will freely estimate the variance of the slope latent factor. The update to the previous model specifications is preceded with a ### annotation. Specifically, we will relax the constraint on the variance of the slope latent factor (s_RC) in order to freely estimate it, which requires removing 0*, such that the resulting line is now: s_RC ~~ s_RC. Beyond that, we will change the model specification object name to lgm_mod4 and the fitted model object to lgm_fit4 for subsequent model comparison purposes.

# Specify freely estimated slope factor variance & assign to object
lgm_mod4 <- "
# Specify and constrain intercept factor loadings
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m 

# Specify and constrain slope factor loadings to linear growth
s_RC =~ 0*RC_1m  + 2*RC_3m  + 5*RC_6m  + 8*RC_9m

# Freely estimate mean of intercept latent factor
i_RC ~ 1

# Freely estimate mean of slope latent factor
s_RC ~ 1

# Freely estimate intercept latent factor variance (allow to vary)
i_RC ~~ i_RC

### Freely estimate slope latent factor variance (allow to vary)
s_RC ~~ s_RC

# Constrain covariance between intercept & slope latent factors to zero
i_RC ~~ 0*s_RC

# Constrain (residual) error variances to be equal (homogeneity of variances)
RC_1m ~~ e*RC_1m
RC_3m ~~ e*RC_3m
RC_6m ~~ e*RC_6m
RC_9m ~~ e*RC_9m
"

# Estimate LGM & assign to fitted model object
lgm_fit4  <- growth(lgm_mod4,  # name of specified model object
                    data=df)   # name of wide-format data frame object
                   
# Print summary of model results
summary(lgm_fit4,              # name of fitted model object
        fit.measures=TRUE,     # request model fit indices
        standardized=TRUE)     # request standardized estimates

## lavaan 0.6.15 ended normally after 29 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         8
##   Number of equality constraints                     3
## 
##   Number of observations                           650
## 
## Model Test User Model:
##                                                       
##   Test statistic                                15.917
##   Degrees of freedom                                 9
##   P-value (Chi-square)                           0.069
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1226.041
##   Degrees of freedom                                 6
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.994
##   Tucker-Lewis Index (TLI)                       0.996
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -10106.661
##   Loglikelihood unrestricted model (H1)     -10098.702
##                                                       
##   Akaike (AIC)                               20223.322
##   Bayesian (BIC)                             20245.707
##   Sample-size adjusted Bayesian (SABIC)      20229.832
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.034
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.062
##   P-value H_0: RMSEA <= 0.050                    0.807
##   P-value H_0: RMSEA >= 0.080                    0.002
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.047
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                              11.686    0.793
##     RC_3m             1.000                              11.686    0.791
##     RC_6m             1.000                              11.686    0.781
##     RC_9m             1.000                              11.686    0.763
##   s_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             2.000                               1.040    0.070
##     RC_6m             5.000                               2.600    0.174
##     RC_9m             8.000                               4.159    0.272
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC              0.000                               0.000    0.000
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC             35.144    0.537   65.429    0.000    3.007    3.007
##     s_RC              4.976    0.062   80.842    0.000    9.571    9.571
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC            136.556    8.977   15.211    0.000    1.000    1.000
##     s_RC              0.270    0.131    2.059    0.039    1.000    1.000
##    .RC_1m      (e)   80.578    2.976   27.074    0.000   80.578    0.371
##    .RC_3m      (e)   80.578    2.976   27.074    0.000   80.578    0.369
##    .RC_6m      (e)   80.578    2.976   27.074    0.000   80.578    0.360
##    .RC_9m      (e)   80.578    2.976   27.074    0.000   80.578    0.344

# Visualize the LGM as a path diagram
semPaths(lgm_fit4,             # name of fitted model object 
         what="est",           # display unstandardized parameter estimates
         weighted=FALSE,       # do not weight plot features
         nCharNodes=0)         # do not abbreviate names

Below, I’ve expanded upon the previous model comparison table by adding in the model fit information for the model in which we freely estimated the variance of the slope latent factor.

Model	\(\chi^{2}\)	df	p	CFI	TLI	RMSEA	SRMR
Baseline Model	3062.245	12	< .001	.000	-2.500	.625	.877
Free Intercept Variance Model	2997.931	11	< .001	.000	-0.335	.646	.809
Linear Slope Latent Factor Model	20.422	10	.026	.991	.995	.040	.034
Free Slope Variance Model	15.917	9	.069	.994	.996	.034	.047

As you can see above, our model fit mostly improves when we freely estimate the variance of the slope latent factor.

As before, we’ll also estimate the chi-square (\(\chi^{2}\)) difference test, except this time we’ll compare the current model (lgm_fit4) to the previous model (lgm_fit3).

# Nested model comparison using chi-square difference test
anova(lgm_fit4, lgm_fit3)

## 
## Chi-Squared Difference Test
## 
##          Df   AIC   BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)  
## lgm_fit4  9 20223 20246 15.917                                         
## lgm_fit3 10 20226 20244 20.422     4.5046 0.073428       1     0.0338 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The chi-square difference test indicates that the current model fits the data statistically significantly better than previous model (\(\Delta \chi^{2}\) = 4.5046, \(\Delta df\) = 1, \(p\) = .0338). This corroborates what we saw with the direct comparison of model fit indices above.

59.2.6.5 Freely Estimate Covariance Between Intercept & Slope Latent Factors

For this model, we will update our previous model by allowing the intercept and slope latent factors to covary; in other words, we will freely estimate the covariance between the intercept and slope latent factors. The update to the previous model specifications is preceded with a ### annotation. Specifically, we will relax the constraint on the covariance in order to freely estimate it, which requires removing 0*, such that the resulting line is now: i_RC ~~ s_RC. Beyond that, we will change the model specification object name to lgm_mod5 and the fitted model object to lgm_fit5 for subsequent model comparison purposes.

# Freely estimate covariance between intercept & slope latent factors & assign to object
lgm_mod5 <- "
# Specify and constrain intercept factor loadings
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m 

# Specify and constrain slope factor loadings to linear growth
s_RC =~ 0*RC_1m  + 2*RC_3m  + 5*RC_6m  + 8*RC_9m

# Freely estimate mean of intercept latent factor
i_RC ~ 1

# Freely estimate mean of slope latent factor
s_RC ~ 1

# Freely estimate intercept latent factor variance (allow to vary)
i_RC ~~ i_RC

# Freely estimate slope latent factor variance (allow to vary)
s_RC ~~ s_RC

### Freely estimate covariance between intercept & slope latent factors
i_RC ~~ s_RC

# Constrain (residual) error variances to be equal (homogeneity of variances)
RC_1m ~~ e*RC_1m
RC_3m ~~ e*RC_3m
RC_6m ~~ e*RC_6m
RC_9m ~~ e*RC_9m
"

# Estimate LGM & assign to fitted model object
lgm_fit5  <- growth(lgm_mod5,  # name of specified model object
                    data=df)   # name of wide-format data frame object
                   
# Print summary of model results
summary(lgm_fit5,              # name of fitted model object
        fit.measures=TRUE,     # request model fit indices
        standardized=TRUE)     # request standardized estimates

## lavaan 0.6.15 ended normally after 38 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         9
##   Number of equality constraints                     3
## 
##   Number of observations                           650
## 
## Model Test User Model:
##                                                       
##   Test statistic                                 6.220
##   Degrees of freedom                                 8
##   P-value (Chi-square)                           0.623
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1226.041
##   Degrees of freedom                                 6
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    1.000
##   Tucker-Lewis Index (TLI)                       1.001
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -10101.812
##   Loglikelihood unrestricted model (H1)     -10098.702
##                                                       
##   Akaike (AIC)                               20215.625
##   Bayesian (BIC)                             20242.487
##   Sample-size adjusted Bayesian (SABIC)      20223.437
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.000
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.039
##   P-value H_0: RMSEA <= 0.050                    0.989
##   P-value H_0: RMSEA >= 0.080                    0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.028
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                              12.433    0.817
##     RC_3m             1.000                              12.433    0.835
##     RC_6m             1.000                              12.433    0.847
##     RC_9m             1.000                              12.433    0.840
##   s_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             2.000                               1.512    0.102
##     RC_6m             5.000                               3.780    0.258
##     RC_9m             8.000                               6.048    0.409
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC             -3.074    1.056   -2.910    0.004   -0.327   -0.327
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC             35.144    0.559   62.824    0.000    2.827    2.827
##     s_RC              4.976    0.064   77.623    0.000    6.582    6.582
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC            154.590   11.444   13.508    0.000    1.000    1.000
##     s_RC              0.572    0.170    3.372    0.001    1.000    1.000
##    .RC_1m      (e)   77.167    3.027   25.495    0.000   77.167    0.333
##    .RC_3m      (e)   77.167    3.027   25.495    0.000   77.167    0.348
##    .RC_6m      (e)   77.167    3.027   25.495    0.000   77.167    0.358
##    .RC_9m      (e)   77.167    3.027   25.495    0.000   77.167    0.352

# Visualize the LGM as a path diagram
semPaths(lgm_fit5,             # name of fitted model object 
         what="est",           # display unstandardized parameter estimates
         weighted=FALSE,       # do not weight plot features
         nCharNodes=0)         # do not abbreviate names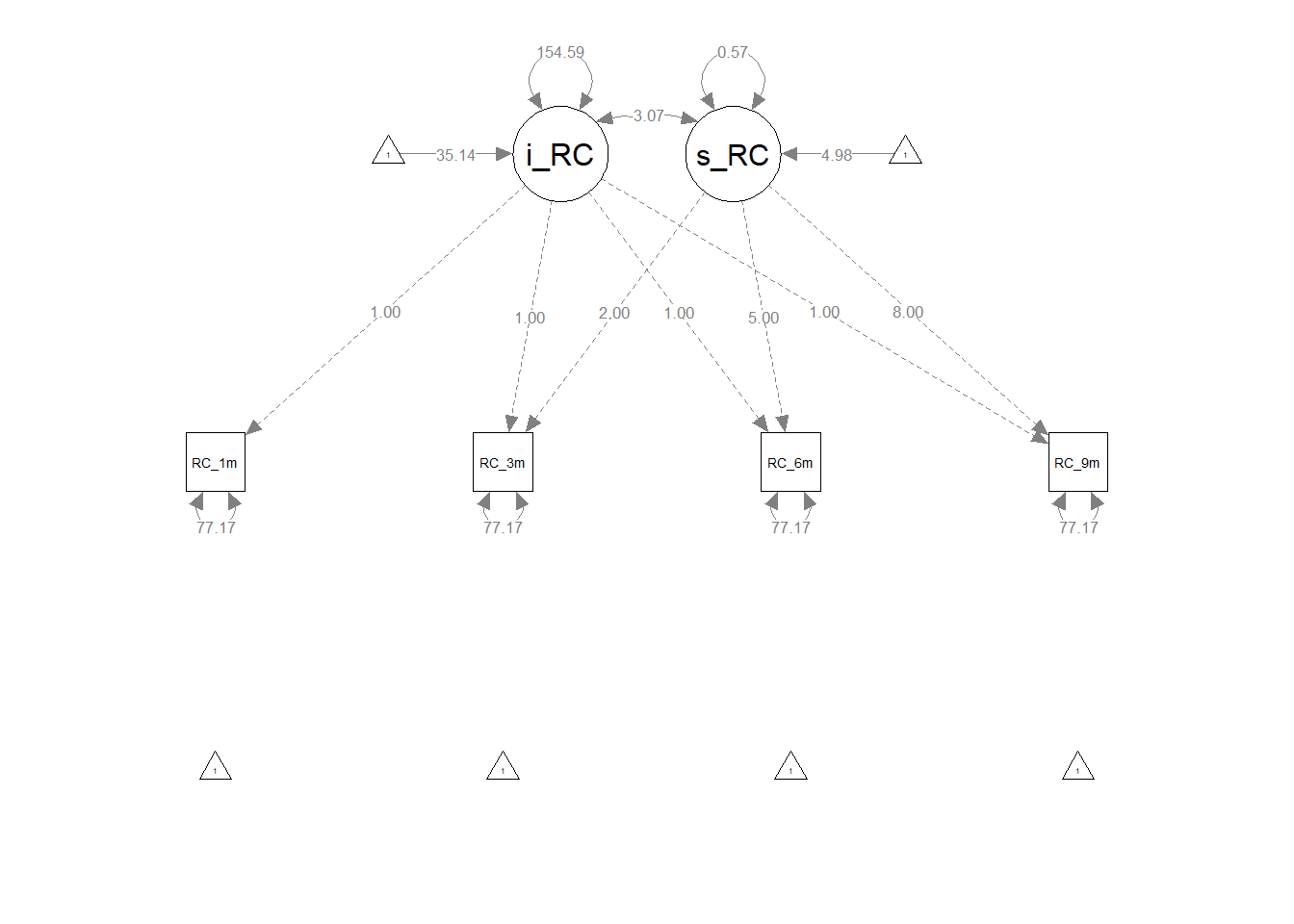

Below, I’ve expanded upon the previous model comparison table by adding in the model fit information for the model in which we freely estimated the covariance between the intercept and slope latent factors.

Model	\(\chi^{2}\)	df	p	CFI	TLI	RMSEA	SRMR
Baseline Model	3062.245	12	< .001	.000	-2.500	.625	.877
Free Intercept Variance Model	2997.931	11	< .001	.000	-0.335	.646	.809
Linear Slope Latent Factor Model	20.422	10	.026	.991	.995	.040	.034
Free Slope Variance Model	15.917	9	.069	.994	.996	.034	.047
Free Covariance Model	6.220	8	.623	1.000	1.001	.000	.028

As you can see above, our model fit improves when we freely estimate the covariance between the intercept and slope latent factors.

As before, we’ll also estimate the chi-square (\(\chi^{2}\)) difference test, except this time we’ll compare the current model (lgm_fit5) to the previous model (lgm_fit4).

# Nested model comparison using chi-square difference test
anova(lgm_fit5, lgm_fit4)

## 
## Chi-Squared Difference Test
## 
##          Df   AIC   BIC   Chisq Chisq diff   RMSEA Df diff Pr(>Chisq)   
## lgm_fit5  8 20216 20243  6.2203                                         
## lgm_fit4  9 20223 20246 15.9171     9.6968 0.11567       1   0.001846 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The chi-square difference test indicates that the current model fits the data statistically significantly better than previous model (\(\Delta \chi^{2}\) = 9.6968, \(\Delta df\) = 1, \(p\) = .001846). This corroborates what we saw with the direct comparison of model fit indices above.

59.2.6.6 Freely Estimate Residual Error Variances

For this final model, we will update our previous model by removing the quality constraints from the (residual) error variances. In other words, we will allow each observed variable’s error variance to be freely estimated. The update to the previous model specifications is preceded with a ### annotation. Specifically, we will relax the quality constraints by removing e* within each error variance term specification. For example, the first observed variable’s error variance should now be specified as: RC_1m ~~ RC_1m. Beyond that, we will change the model specification object name to lgm_mod6 and the fitted model object to lgm_fit6 for subsequent model comparison purposes.

# Freely estimate residual error variances & assign to object
lgm_mod6 <- "
# Specify and constrain intercept factor loadings
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m 

# Specify and constrain slope factor loadings to linear growth
s_RC =~ 0*RC_1m  + 2*RC_3m  + 5*RC_6m  + 8*RC_9m

# Freely estimate mean of intercept latent factor
i_RC ~ 1

# Freely estimate mean of slope latent factor
s_RC ~ 1

# Freely estimate intercept latent factor variance (allow to vary)
i_RC ~~ i_RC

# Freely estimate slope latent factor variance (allow to vary)
s_RC ~~ s_RC

# Freely estimate covariance between intercept & slope latent factors
i_RC ~~ s_RC

### Freely estimate error variances (heterogeneity of variances)
RC_1m ~~ RC_1m
RC_3m ~~ RC_3m
RC_6m ~~ RC_6m
RC_9m ~~ RC_9m
"

# Estimate LGM & assign to fitted model object
lgm_fit6  <- growth(lgm_mod6,  # name of specified model object
                    data=df)   # name of wide-format data frame object
                   
# Print summary of model results
summary(lgm_fit6,              # name of fitted model object
        fit.measures=TRUE,     # request model fit indices
        standardized=TRUE)     # request standardized estimates

## lavaan 0.6.15 ended normally after 96 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         9
## 
##   Number of observations                           650
## 
## Model Test User Model:
##                                                       
##   Test statistic                                 3.760
##   Degrees of freedom                                 5
##   P-value (Chi-square)                           0.584
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1226.041
##   Degrees of freedom                                 6
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    1.000
##   Tucker-Lewis Index (TLI)                       1.001
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -10100.582
##   Loglikelihood unrestricted model (H1)     -10098.702
##                                                       
##   Akaike (AIC)                               20219.165
##   Bayesian (BIC)                             20259.458
##   Sample-size adjusted Bayesian (SABIC)      20230.883
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.000
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.047
##   P-value H_0: RMSEA <= 0.050                    0.963
##   P-value H_0: RMSEA >= 0.080                    0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.019
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                              12.463    0.820
##     RC_3m             1.000                              12.463    0.834
##     RC_6m             1.000                              12.463    0.840
##     RC_9m             1.000                              12.463    0.855
##   s_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             2.000                               1.725    0.116
##     RC_6m             5.000                               4.314    0.291
##     RC_9m             8.000                               6.902    0.474
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC             -3.483    1.147   -3.036    0.002   -0.324   -0.324
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC             35.143    0.559   62.824    0.000    2.820    2.820
##     s_RC              4.975    0.064   77.667    0.000    5.767    5.767
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##     i_RC            155.324   11.703   13.273    0.000    1.000    1.000
##     s_RC              0.744    0.211    3.520    0.000    1.000    1.000
##    .RC_1m            75.459    7.345   10.273    0.000   75.459    0.327
##    .RC_3m            78.779    5.811   13.557    0.000   78.779    0.353
##    .RC_6m            81.083    5.791   14.001    0.000   81.083    0.368
##    .RC_9m            65.214    7.998    8.154    0.000   65.214    0.307

# Visualize the LGM as a path diagram
semPaths(lgm_fit6,             # name of fitted model object 
         what="est",           # display unstandardized parameter estimates
         weighted=FALSE,       # do not weight plot features
         nCharNodes=0)         # do not abbreviate names

Below, I’ve expanded upon the previous model comparison table by adding in the model fit information for model in which we relaxed the homogeneity of variances constraint.

Model	\(\chi^{2}\)	df	p	CFI	TLI	RMSEA	SRMR
Baseline Model	3062.245	12	< .001	.000	-2.500	.625	.877
Free Intercept Variance Model	2997.931	11	< .001	.000	-0.335	.646	.809
Linear Slope Latent Factor Model	20.422	10	.026	.991	.995	.040	.034
Free Slope Variance Model	15.917	9	.069	.994	.996	.034	.047
Free Covariance Model	6.220	8	.623	1.000	1.001	.000	.028
Free Residual Error Variances Model	3.760	5	.584	1.000	1.001	.000	.019

As you can see above, some model fit indices improved or stayed about the same when we freely estimate each of the residual error variances associated with the observed variables.

As before, we’ll also estimate the chi-square (\(\chi^{2}\)) difference test, except this time we’ll compare the current model (lgm_fit6) to the previous model (lgm_fit5).

# Nested model comparison using chi-square difference test
anova(lgm_fit6, lgm_fit5)

## 
## Chi-Squared Difference Test
## 
##          Df   AIC   BIC  Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
## lgm_fit6  5 20219 20260 3.7603                                    
## lgm_fit5  8 20216 20243 6.2203       2.46     0       3     0.4826

The chi-square difference test indicates that the current model fits the data about the same as than previous model (\(\Delta \chi^{2}\) = 2.46, \(\Delta df\) = 3, \(p\) = .4826). This suggests that we should go with the simpler model (lgm_fit5) in which residual error variances were constrained to be equal.

59.2.6.7 Create a Matrix Comparing Model Fit Indices

If our goals are to create a matrix containing only those model fit indices that we covered in this chapter and to add in the chi-square difference tests, we can do the following, which incorporates the inspect function from the lavaan package and the cbind, rbind, and t functions from base R.

# Create object containing selected fit indices
select_fit_indices <- c("chisq","df","pvalue","cfi","tli","rmsea","srmr")

# Create matrix comparing model fit indices
compare_mods <- cbind(
  inspect(lgm_fit1, "fit.indices")[select_fit_indices],
  inspect(lgm_fit2, "fit.indices")[select_fit_indices],
  inspect(lgm_fit3, "fit.indices")[select_fit_indices], 
  inspect(lgm_fit4, "fit.indices")[select_fit_indices], 
  inspect(lgm_fit5, "fit.indices")[select_fit_indices], 
  inspect(lgm_fit6, "fit.indices")[select_fit_indices]
  )

# Add more informative model names to matrix columns
colnames(compare_mods) <- c("Baseline Model", 
                            "Free Intercept Variance Model",
                            "Linear Slope Latent Factor Model",
                            "Free Slope Variance Model",
                            "Free Covariance Model",
                            "Free Residual Error Variances Model")

# Create vector of chi-square difference tests (nested model comparisons)
`chisq diff (p-value)` <- c(NA,
                            anova(lgm_fit2, lgm_fit1)$`Pr(>Chisq)`[2],
                            anova(lgm_fit3, lgm_fit2)$`Pr(>Chisq)`[2],
                            anova(lgm_fit4, lgm_fit3)$`Pr(>Chisq)`[2],
                            anova(lgm_fit5, lgm_fit4)$`Pr(>Chisq)`[2],
                            anova(lgm_fit6, lgm_fit5)$`Pr(>Chisq)`[2])

# Add chi-square difference tests to matrix object
compare_mods <- rbind(compare_mods, `chisq diff (p-value)`)

# Round object values to 3 places after decimal
compare_mods <- round(compare_mods, 3)

# Rotate matrix
compare_mods <- t(compare_mods)

# Print object
print(compare_mods)

##                                        chisq df pvalue   cfi    tli rmsea  srmr chisq diff (p-value)
## Baseline Model                      3062.245 12  0.000 0.000 -0.250 0.625 0.877                   NA
## Free Intercept Variance Model       2997.931 11  0.000 0.000 -0.335 0.646 0.809                0.000
## Linear Slope Latent Factor Model      20.422 10  0.026 0.991  0.995 0.040 0.034                0.000
## Free Slope Variance Model             15.917  9  0.069 0.994  0.996 0.034 0.047                0.034
## Free Covariance Model                  6.220  8  0.623 1.000  1.001 0.000 0.028                0.002
## Free Residual Error Variances Model    3.760  5  0.584 1.000  1.001 0.000 0.019                0.483

59.2.7 Estimate Nonlinear Latent Growth Models

Thus far in the chapter we have focused on estimating models in which change is constrained to be linear. In this section, we will learn how to specify quadratic and cubic models, which are examples of nonlinear functional forms.

59.2.7.1 Estimate Quadratic Latent Growth Model

Just as we did with the conditional unconstrained LGM with a linear functional form in a previous section, first, we must specify the LGM and assign it to an object that we can subsequently reference. To do so, we will do the following.

1. Specify a name for the model object (e.g., lgm_mod_quad), followed by the <- assignment operator.
2. To the right of the <- assignment operator and within quotation marks (" "):
3. Specify a name for the intercept latent factor (e.g., i_RC), followed by the =~ operator, which is used to indicate how a latent factor is measured. Anything that comes to the right of the =~ operator is an observed variable (i.e., indicator) of the latent factor. Please note that the latent factor is not something that we directly observe, so it will not have a corresponding variable in our data frame object.

1. After the =~ operator, specify each observed variable associated with the intercept latent factor, and to separate the observed variables, insert the + operator. In this example, the four observed variables are: RC_1m, RC_3m, RC_6m, and RC_9m. These are our observed variables, which conceptually are influenced by the underlying latent factor.
2. To set the i_RC latent factor as the intercept, we also need to constrain each observed variable’s factor loading to 1 by preceding each observed variable by 1*. As a result, the end result should look like this: i_RC =~ 1*RC_1m + 1*RC_3m + 1*RC_6m + 1*RC_9m.

4. Specify a name for the linear slope latent factor (e.g., s_RC), followed by the =~ operator, which is used to indicate how a latent factor is measured.

1. After the =~ operator, specify each observed variable associated with the slope latent factor, which will be the same observed variables that serve as indicators for the intercept latent factor. To separate the observed variables, insert the + operator.
2. To set the s_RC latent factor as the linear slope, we also need to constrain each observed variable’s factor loading to account for the time intervals between measurement occasions, which is also known as time coding. Because role clarity was measured at 1 month, 3 months, 6 months, and 9 months, we will subtract 1 from each month, which will result in the 1-month measurement occasion becoming 0 and thus setting a measurement occasion to serve as the intercept value; in other words, conceptually, the measurement occasion coded as 0 represents the value of role clarity when its slope crosses time equal to 0. Subtracting 1 from each measurement occasion in this example also allows for us to account for the unequal time intervals associated with the measurement occasions. As a result, the end result should look like this: s_RC =~ 0*RC_1m + 2*RC_3m + 5*RC_6m + 8*RC_9m.
3. Note: We could have specified a different measurement occasion slope factor loading as 0 by simply changing the time coding; for example, if we were to set the last measurement occasion slope factor loading as 0, our time coding would be: s_RC =~ -8*RC_1m + -6*RC_3m + -3*RC_6m + 0*RC_9m. Finally, if the time intervals between measurement occasions had been equal, we would have been able to apply a 0, 1, 2, and 3 time coding for the slope factor loadings to set the intercept at the first measurement occasion, or -3, -2, -1, and 0 to set the intercept at the last measurement occasion.

4. Specify a name for the quadratic slope latent factor (e.g., q_RC), followed by the =~ operator, which is used to indicate how a latent factor is measured.

1. After the =~ operator, specify each observed variable associated with the slope latent factor, which will be the same observed variables that serve as indicators for the intercept and linear slope latent factors. To separate the observed variables, insert the + operator.
2. To set the q_RC latent factor as the quadratic slope, we also need to constrain each observed variable’s factor loading to account for the time intervals between measurement occasion. Specifically, we need to square each of the factor loading constrains from our linear slope factor. As a result, the end result should look like this: q_RC =~ 0*RC_1m + 4*RC_3m + 25*RC_6m + 64*RC_9m.

# Specify unconditional unconstrained quadratic LGM & assign to object
lgm_mod_quad <- "
# Specify and constrain intercept factor loadings
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m

# Specify and constrain linear slope factor loadings
s_RC =~ 0*RC_1m  + 2*RC_3m  + 5*RC_6m  + 8*RC_9m

# Specify and constrain quadratic slope factor loadings
q_RC =~ 0*RC_1m  + 4*RC_3m  + 25*RC_6m  + 64*RC_9m
"

Second, now that we have specified the model object (lgm_mod_quad), we are ready to estimate the model using the growth function from the lavaan package. To do so, we will do the following.

1. Specify a name for the fitted model object (e.g., lgm_fit_quad), followed by the <- assignment operator.
2. To the right of the <- assignment operator, type the name of the growth function, and within the function parentheses include the following arguments.

1. As the first argument, insert the name of the model object that we specified above (lgm_mod_quad).
2. As the second argument, insert the name of the data frame object to which the indicator variables in our model belong. That is, after data=, insert the name of the original wide-format data frame object (df).
3. Note: The growth function includes model estimation defaults, which explains why we had relatively few model specifications.

# Estimate unconditional unconstrained quadratic LGM & assign to fitted model object
lgm_fit_quad <- growth(lgm_mod_quad, # name of specified model object
                       data=df)      # name of wide-format data frame object

Third, we will use the summary function from base R to to print the model results. To do so, we will apply the following arguments in the summary function parentheses.

1. As the first argument, specify the name of the fitted model object that we created above (lgm_fit_quad).
2. As the second argument, set fit.measures=TRUE to obtain the model fit indices (e.g., CFI, TLI, RMSEA, SRMR).
3. As the third argument, set standardized=TRUE to request the standardized parameter estimates for the model.

# Print summary of model results
summary(lgm_fit_quad,        # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE)   # request standardized estimates

## lavaan 0.6.15 ended normally after 146 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        13
## 
##   Number of observations                           650
## 
## Model Test User Model:
##                                                       
##   Test statistic                                 0.026
##   Degrees of freedom                                 1
##   P-value (Chi-square)                           0.872
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1226.041
##   Degrees of freedom                                 6
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    1.000
##   Tucker-Lewis Index (TLI)                       1.005
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -10098.715
##   Loglikelihood unrestricted model (H1)     -10098.702
##                                                       
##   Akaike (AIC)                               20223.431
##   Bayesian (BIC)                             20281.631
##   Sample-size adjusted Bayesian (SABIC)      20240.357
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.000
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.054
##   P-value H_0: RMSEA <= 0.050                    0.943
##   P-value H_0: RMSEA >= 0.080                    0.016
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.001
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                              12.200    0.814
##     RC_3m             1.000                              12.200    0.809
##     RC_6m             1.000                              12.200    0.809
##     RC_9m             1.000                              12.200    0.846
##   s_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             2.000                               3.143    0.208
##     RC_6m             5.000                               7.858    0.521
##     RC_9m             8.000                              12.572    0.872
##   q_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             4.000                               0.707    0.047
##     RC_6m            25.000                               4.421    0.293
##     RC_9m            64.000                              11.319    0.785
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC             -0.194    7.101   -0.027    0.978   -0.010   -0.010
##     q_RC             -0.391    0.696   -0.562    0.574   -0.181   -0.181
##   s_RC ~~                                                               
##     q_RC             -0.230    0.347   -0.662    0.508   -0.827   -0.827
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
##     i_RC             35.055    0.577   60.704    0.000    2.873    2.873
##     s_RC              5.079    0.217   23.378    0.000    3.232    3.232
##     q_RC             -0.013    0.025   -0.501    0.617   -0.072   -0.072
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m            76.049   15.967    4.763    0.000   76.049    0.338
##    .RC_3m            75.815    7.696    9.851    0.000   75.815    0.333
##    .RC_6m            76.478    9.370    8.162    0.000   76.478    0.336
##    .RC_9m            61.428   27.256    2.254    0.024   61.428    0.295
##     i_RC            148.840   17.473    8.518    0.000    1.000    1.000
##     s_RC              2.470    3.613    0.683    0.494    1.000    1.000
##     q_RC              0.031    0.039    0.799    0.424    1.000    1.000

With respect to model fit, the model fit indices suggest acceptable fit to the data. With respect to the parameter estimates, we’ll focus on just the means of the latent factors. Notably, the unstandardized means of the intercept and linear slope latent factors are statistically significant (35.055, p < .001 and 5.079, p < .001); however, the newly introduced quadratic slope latent factor is not statistically significant (-0.013, p = .617), which suggests that the added quadratic term does not explain any additional information beyond what the the means of the intercept and linear slope latent factors already explain. Thus, we can conclude that there does not appear to be a quadratic functional form associated with the average growth trajectory for role clarity. Had the mean of the quadratic slope latent factor been statistically significant, it would have indicated that the functional form is quadratic, but that’s not the case here.

Because our original unconditional constrained linear LGM from an earlier section is nested with the this quadratic LGM, we can perform a nested model comparison using the chi-square difference test. To perform this test, we’ll apply the anova function from base R to our two fitted model objects. As the first argument, we’ll insert the name of our model containing the current quadratic fitted model object (lgm_fit_quad), and as the second argument, we’ll insert the name of our linear fitted model object (lgm_fit).

# Nested model comparison using chi-square difference test
anova(lgm_fit_quad, lgm_fit)

## 
## Chi-Squared Difference Test
## 
##              Df   AIC   BIC  Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
## lgm_fit_quad  1 20223 20282 0.0261                                    
## lgm_fit       5 20219 20260 3.7603     3.7342     0       4     0.4432

The chi-square difference test indicates that the more parsimonious linear LGM does not fit the data statistically significantly worse than the current more complex quadratic LGM (\(\Delta \chi^{2}\) = 3.7342, \(\Delta df\) = 4, \(p\) = .4432). Thus, we should retain the linear LGM instead of the quadratic LGM.

59.2.7.2 Estimate Cubic Latent Growth Model

Estimating a cubic function form for an LGM requires adding a cubic slope latent factor to the quadratic LGM we specified in the previous section (e.g., c_RC). To do so, we cube the linear slope factor loading constraints, which will result in the following: c_RC =~ 0*RC_1m + 8*RC_3m + 125*RC_6m + 512*RC_9m.

# Specify unconditional unconstrained cubic LGM & assign to object
lgm_mod_cubic <- "
# Specify and constrain intercept factor loadings
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m

# Specify and constrain linear slope factor loadings
s_RC =~ 0*RC_1m  + 2*RC_3m  + 5*RC_6m  + 8*RC_9m

# Specify and constrain quadratic slope factor loadings
q_RC =~ 0*RC_1m  + 4*RC_3m  + 25*RC_6m  + 64*RC_9m

# Specify and constrain cubic slope factor loadings
c_RC =~ 0*RC_1m  + 8*RC_3m  + 125*RC_6m  + 512*RC_9m
"

To estimate the fitted model, we follow the same process as the linear LGM and quadratic LGM, except we insert the name of the new lgm_mod_cubic specified model object as the first argument in the growth function, and we assign the resulting fitted model to an object that we’ll call lgm_fit_cubic.

# Estimate unconditional unconstrained cubic LGM & assign to fitted model object
lgm_fit_cubic <- growth(lgm_mod_cubic, # name of specified model object
                        data=df)       # name of wide-format data frame object

As we did previously, we use the summary function to print a summary of the model fit and parameter estimates results, except we insert the cubic LGM fitted model object (lgm_fit_cubic) as the first argument in the function.

# Print summary of model results
summary(lgm_fit_cubic,       # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE)   # request standardized estimates

## lavaan 0.6.15 ended normally after 177 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        18
## 
##   Number of observations                           650
## 
## Model Test User Model:
##                                                       
##   Test statistic                                    NA
##   Degrees of freedom                                -4
##   P-value (Unknown)                                 NA
## 
## Model Test Baseline Model:
## 
##   Test statistic                                    NA
##   Degrees of freedom                                NA
##   P-value                                           NA
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                       NA
##   Tucker-Lewis Index (TLI)                          NA
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -10098.702
##   Loglikelihood unrestricted model (H1)     -10098.702
##                                                       
##   Akaike (AIC)                               20233.405
##   Bayesian (BIC)                             20313.990
##   Sample-size adjusted Bayesian (SABIC)      20256.841
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.000
##   90 Percent confidence interval - lower            NA
##   90 Percent confidence interval - upper            NA
##   P-value H_0: RMSEA <= 0.050                       NA
##   P-value H_0: RMSEA >= 0.080                       NA
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.000
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                               7.881    0.526
##     RC_3m             1.000                               7.881    0.523
##     RC_6m             1.000                               7.881    0.522
##     RC_9m             1.000                               7.881    0.546
##   s_RC =~                                                               
##     RC_1m             0.000                                  NA       NA
##     RC_3m             2.000                                  NA       NA
##     RC_6m             5.000                                  NA       NA
##     RC_9m             8.000                                  NA       NA
##   q_RC =~                                                               
##     RC_1m             0.000                                  NA       NA
##     RC_3m             4.000                                  NA       NA
##     RC_6m            25.000                                  NA       NA
##     RC_9m            64.000                                  NA       NA
##   c_RC =~                                                               
##     RC_1m             0.000                                  NA       NA
##     RC_3m             8.000                                  NA       NA
##     RC_6m           125.000                                  NA       NA
##     RC_9m           512.000                                  NA       NA
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC             71.363       NA                     19.933   19.933
##     q_RC            -16.655       NA                     -2.214   -2.214
##     c_RC              1.084       NA                      0.895    0.895
##   s_RC ~~                                                               
##     q_RC             -1.087       NA                     -2.507   -2.507
##     c_RC              0.003       NA                      0.047    0.047
##   q_RC ~~                                                               
##     c_RC              0.167       NA                      1.138    1.138
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
##     i_RC             35.037       NA                      4.446    4.446
##     s_RC              5.151       NA                         NA       NA
##     q_RC             -0.038       NA                         NA       NA
##     c_RC              0.002       NA                         NA       NA
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m           162.783       NA                    162.783    0.724
##    .RC_3m            19.290       NA                     19.290    0.085
##    .RC_6m           180.973       NA                    180.973    0.795
##    .RC_9m           105.095       NA                    105.095    0.505
##     i_RC             62.105       NA                      1.000    1.000
##     s_RC             -0.206       NA                         NA       NA
##     q_RC             -0.911       NA                         NA       NA
##     c_RC             -0.024       NA                         NA       NA

In the output, note how the degrees of freedom for the cubic LGM is -4. This indicates that the cubic model is under-identified, and thus we can’t estimate the model’s fit to the data or the standard errors of its freely estimated parameters. To estimate an over-identified cubic LGM, we would need at least five measurement occasions. Had our cubic LGM been over-identified, we would have looked at the statistical significance of the mean of the cubic slope factor to determine whether the model showed evidence of a cubic functional form; further, we would have then been able to perform a nested model comparison with the quadratic LGM.

59.2.8 Estimating Models with Missing Data

When missing data are present, we must carefully consider how we handle the missing data before or during the estimations of a model. In the chapter on missing data, I provide an overview of relevant concepts, particularly if the data are missing completely at random (MCAR), missing at random (MAR), or missing not at random (MNAR); I suggest reviewing that chapter prior to handling missing data.

As a potential method for addressing missing data, the lavaan model functions, such as the growth function, allow for full-information maximum likelihood (FIML). Further, the functions allow us to specify specific estimators given the type of data we wish to use for model estimation (e.g., ML, MLR).

To demonstrate how missing data are handled using FIML, we will need to first introduce some missing data into our data. To do so, we will use a multiple imputation package called mice and a function called ampute that “amputates” existing data by creating missing data patterns. For our purposes, we’ll replace 10% (.1) of data frame cells with NA (which is signifies a missing value) such that the missing data are missing completely at random (MCAR).

# Install package
install.packages("mice")

# Access package
library(mice)

# Create a new data frame object
df_missing <- df

# Remove non-numeric variable(s) from data frame object
df_missing$EmployeeID <- NULL

# Set a seed
set.seed(2024)

# Remove 10% of cells so missing data are MCAR
df_missing <- ampute(df_missing, prop=.1, mech="MCAR")

# Extract the new missing data frame object and overwrite existing object
df_missing <- df_missing$amp

Implementing FIML when missing data are present is relatively straightforward. For example, for the unconditional unconstrained LGM from a previous section, we can apply FIML in the presence of missing data by adding the missing="fiml" argument to the growth function.

# Specify unconditional unconstrained LGM & assign to object
lgm_mod <- "
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m
s_RC =~ 0*RC_1m  + 2*RC_3m  + 5*RC_6m  + 8*RC_9m
"

# Estimate unconditional unconstrained LGM & assign to fitted model object
lgm_fit  <- growth(lgm_mod,         # name of specified model object
                   data=df_missing, # name of wide-format data frame object
                   missing="fiml")  # specify FIML
              
# Print summary of model results
summary(lgm_fit,             # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE)   # request standardized estimates

## lavaan 0.6.15 ended normally after 95 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         9
## 
##   Number of observations                           650
##   Number of missing patterns                         5
## 
## Model Test User Model:
##                                                       
##   Test statistic                                 2.944
##   Degrees of freedom                                 5
##   P-value (Chi-square)                           0.709
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1197.353
##   Degrees of freedom                                 6
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    1.000
##   Tucker-Lewis Index (TLI)                       1.002
##                                                       
##   Robust Comparative Fit Index (CFI)             1.000
##   Robust Tucker-Lewis Index (TLI)                1.002
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)              -9975.174
##   Loglikelihood unrestricted model (H1)      -9973.702
##                                                       
##   Akaike (AIC)                               19968.347
##   Bayesian (BIC)                             20008.640
##   Sample-size adjusted Bayesian (SABIC)      19980.065
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.000
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.041
##   P-value H_0: RMSEA <= 0.050                    0.980
##   P-value H_0: RMSEA >= 0.080                    0.000
##                                                       
##   Robust RMSEA                                   0.000
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.041
##   P-value H_0: Robust RMSEA <= 0.050             0.979
##   P-value H_0: Robust RMSEA >= 0.080             0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.017
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Observed
##   Observed information based on                Hessian
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                              12.563    0.823
##     RC_3m             1.000                              12.563    0.839
##     RC_6m             1.000                              12.563    0.848
##     RC_9m             1.000                              12.563    0.862
##   s_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             2.000                               1.738    0.116
##     RC_6m             5.000                               4.344    0.293
##     RC_9m             8.000                               6.951    0.477
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC             -3.755    1.175   -3.196    0.001   -0.344   -0.344
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
##     i_RC             35.112    0.564   62.222    0.000    2.795    2.795
##     s_RC              4.977    0.065   76.712    0.000    5.728    5.728
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m            75.372    7.497   10.054    0.000   75.372    0.323
##    .RC_3m            78.474    5.890   13.324    0.000   78.474    0.350
##    .RC_6m            80.340    5.810   13.827    0.000   80.340    0.366
##    .RC_9m            66.406    8.148    8.150    0.000   66.406    0.313
##     i_RC            157.819   11.855   13.312    0.000    1.000    1.000
##     s_RC              0.755    0.218    3.459    0.001    1.000    1.000

The FIML approach uses all observations in which data are missing on one or more endogenous variables in the model. As you can see in the output, all 650 observations were retained for estimating the model.

Now watch what happens when we remove the missing="fiml" argument in the presence of missing data.

# Specify unconditional unconstrained LGM & assign to object
lgm_mod <- "
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m
s_RC =~ 0*RC_1m  + 2*RC_3m  + 5*RC_6m  + 8*RC_9m
"

# Estimate unconditional unconstrained LGM & assign to fitted model object
lgm_fit  <- growth(lgm_mod,         # name of specified model object
                   data=df_missing) # name of wide-format data frame object
              
# Print summary of model results
summary(lgm_fit,             # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE)   # request standardized estimates

## lavaan 0.6.15 ended normally after 93 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         9
## 
##                                                   Used       Total
##   Number of observations                           616         650
## 
## Model Test User Model:
##                                                       
##   Test statistic                                 2.389
##   Degrees of freedom                                 5
##   P-value (Chi-square)                           0.793
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1153.818
##   Degrees of freedom                                 6
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    1.000
##   Tucker-Lewis Index (TLI)                       1.003
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)              -9564.632
##   Loglikelihood unrestricted model (H1)      -9563.438
##                                                       
##   Akaike (AIC)                               19147.264
##   Bayesian (BIC)                             19187.074
##   Sample-size adjusted Bayesian (SABIC)      19158.500
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.000
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.036
##   P-value H_0: RMSEA <= 0.050                    0.987
##   P-value H_0: RMSEA >= 0.080                    0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.016
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                              12.523    0.829
##     RC_3m             1.000                              12.523    0.839
##     RC_6m             1.000                              12.523    0.850
##     RC_9m             1.000                              12.523    0.863
##   s_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             2.000                               1.740    0.117
##     RC_6m             5.000                               4.350    0.295
##     RC_9m             8.000                               6.960    0.480
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC             -3.916    1.185   -3.304    0.001   -0.359   -0.359
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
##     i_RC             35.324    0.575   61.481    0.000    2.821    2.821
##     s_RC              4.963    0.066   75.250    0.000    5.704    5.704
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m            71.546    7.371    9.706    0.000   71.546    0.313
##    .RC_3m            78.644    5.953   13.211    0.000   78.644    0.353
##    .RC_6m            80.307    5.890   13.634    0.000   80.307    0.370
##    .RC_9m            68.051    8.281    8.218    0.000   68.051    0.323
##     i_RC            156.837   12.022   13.046    0.000    1.000    1.000
##     s_RC              0.757    0.217    3.495    0.000    1.000    1.000

As you can see in the output, the growth function defaults to listwise deletion when we do not specify that FIML be applied. This results in the number of observations dropping from 650 to 616 for model estimation purposes. A reduction in sample size can negatively affect our statistical power to detect associations or effects that truly exist in the underlying population. To learn more about statistical power, please refer to the chapter on power analysis.

Within the growth function, we can also specify a specific estimator if we choose to override the default. For example, we could specify the MLR (maximum likelihood with robust standard errors) estimator if we had good reason to. To do so, we would add this argument: estimator="MLR". For a list of other available estimators, you can check out the lavaan package website.

# Specify unconditional unconstrained LGM & assign to object
lgm_mod <- "
i_RC =~ 1*RC_1m  + 1*RC_3m  + 1*RC_6m  + 1*RC_9m
s_RC =~ 0*RC_1m  + 2*RC_3m  + 5*RC_6m  + 8*RC_9m
"

# Estimate unconditional unconstrained LGM & assign to fitted model object
lgm_fit  <- growth(lgm_mod,         # name of specified model object
                   data=df_missing, # name of wide-format data frame object
                   estimator="MLR", # specify MLR estimator
                   missing="fiml")  # specify FIML
              
# Print summary of model results
summary(lgm_fit,             # name of fitted model object
        fit.measures=TRUE,   # request model fit indices
        standardized=TRUE)   # request standardized estimates

## lavaan 0.6.15 ended normally after 95 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                         9
## 
##   Number of observations                           650
##   Number of missing patterns                         5
## 
## Model Test User Model:
##                                               Standard      Scaled
##   Test Statistic                                 2.944       3.078
##   Degrees of freedom                                 5           5
##   P-value (Chi-square)                           0.709       0.688
##   Scaling correction factor                                  0.957
##     Yuan-Bentler correction (Mplus variant)                       
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1197.353    1188.078
##   Degrees of freedom                                 6           6
##   P-value                                        0.000       0.000
##   Scaling correction factor                                  1.008
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    1.000       1.000
##   Tucker-Lewis Index (TLI)                       1.002       1.002
##                                                                   
##   Robust Comparative Fit Index (CFI)                         1.000
##   Robust Tucker-Lewis Index (TLI)                            1.002
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)              -9975.174   -9975.174
##   Scaling correction factor                                  0.953
##       for the MLR correction                                      
##   Loglikelihood unrestricted model (H1)      -9973.702   -9973.702
##   Scaling correction factor                                  0.954
##       for the MLR correction                                      
##                                                                   
##   Akaike (AIC)                               19968.347   19968.347
##   Bayesian (BIC)                             20008.640   20008.640
##   Sample-size adjusted Bayesian (SABIC)      19980.065   19980.065
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.000       0.000
##   90 Percent confidence interval - lower         0.000       0.000
##   90 Percent confidence interval - upper         0.041       0.043
##   P-value H_0: RMSEA <= 0.050                    0.980       0.975
##   P-value H_0: RMSEA >= 0.080                    0.000       0.000
##                                                                   
##   Robust RMSEA                                               0.000
##   90 Percent confidence interval - lower                     0.000
##   90 Percent confidence interval - upper                     0.041
##   P-value H_0: Robust RMSEA <= 0.050                         0.979
##   P-value H_0: Robust RMSEA >= 0.080                         0.000
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.017       0.017
## 
## Parameter Estimates:
## 
##   Standard errors                             Sandwich
##   Information bread                           Observed
##   Observed information based on                Hessian
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC =~                                                               
##     RC_1m             1.000                              12.563    0.823
##     RC_3m             1.000                              12.563    0.839
##     RC_6m             1.000                              12.563    0.848
##     RC_9m             1.000                              12.563    0.862
##   s_RC =~                                                               
##     RC_1m             0.000                               0.000    0.000
##     RC_3m             2.000                               1.738    0.116
##     RC_6m             5.000                               4.344    0.293
##     RC_9m             8.000                               6.951    0.477
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   i_RC ~~                                                               
##     s_RC             -3.755    1.123   -3.344    0.001   -0.344   -0.344
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m             0.000                               0.000    0.000
##    .RC_3m             0.000                               0.000    0.000
##    .RC_6m             0.000                               0.000    0.000
##    .RC_9m             0.000                               0.000    0.000
##     i_RC             35.112    0.564   62.269    0.000    2.795    2.795
##     s_RC              4.977    0.065   76.677    0.000    5.728    5.728
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .RC_1m            75.372    7.199   10.470    0.000   75.372    0.323
##    .RC_3m            78.474    6.076   12.914    0.000   78.474    0.350
##    .RC_6m            80.340    5.632   14.264    0.000   80.340    0.366
##    .RC_9m            66.406    7.892    8.414    0.000   66.406    0.313
##     i_RC            157.819   10.862   14.529    0.000    1.000    1.000
##     s_RC              0.755    0.219    3.443    0.001    1.000    1.000

59.2.9 Summary

In this chapter, we learned how to estimate latent growth models to understand the extent to which individuals’ from a population experience change in a construct over time, compare the fit of nested models, estimate nonlinear models, and estimate models when missing data are present.

References

Bagozzi, Richard P, and Youjae Yi. 1988. “On the Evaluation of Structural Equation Models.” Journal of the Academy of Marketing Science 16: 74–94.

Hu, Li-tze, and Peter M Bentler. 1999. “Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria Versus New Alternatives.” Structural Equation Modeling 6 (1): 1–55.

Kline, Rex B. 2011. Principles and Practice of Structural Equation Modeling (3rd Ed.). New York, New York: The Guilford Press.

Meredith, William, and John Tisak. 1990. “Latent Curve Analysis.” Psychometrika 55 (1): 107–22.

Newsom, Jason T. 2024. Longitudinal Structural Equation Modeling: A Comprehensive Introduction (2nd Ed.). New York, New York: Routledge.

Nye, Christopher D. 2023. “Reviewer Resources: Confirmatory Factor Analysis.” Organizational Research Methods 26 (4): 608–28.

Wickham, Hadley, Jim Hester, and Jennifer Bryan. 2024. Readr: Read Rectangular Text Data. https://CRAN.R-project.org/package=readr.