Chapter 61 Preparing Market Survey Data
In this chapter, we will learn how to prepare market survey data by aging and applying weights to the data.
61.1 Conceptual Overview
A market review refers to the “process of collecting pay data for benchmark jobs from other organizations” (Bauer et al. 2025). When conducting a market review, it is a common practice to acquire data from a market survey, where a market survey (salary survey) refers to a survey used to collect pay data on benchmark jobs (key jobs), which is often conducted by a third-party vendor or government agency. Examples of such third-party parties include traditional surveys (e.g., CareerOneStop.org), customized surveys, and web-based platforms or surveys (e.g., PayScale.com).
The overarching goal of a market review is often to ensure what is called external equity (external competitiveness), which has to do with how competitive an organization’s pay practices are for particular job relative to other competitor organizations. For example, for a given job, an organization might lead, match, or lag the market pay rates for that job. By ensuring external equity in our organization for critical jobs, we will hopefully be better positioned to attract, motivate, and retain talented individuals. In fact, some organization’s adopt adhere to market pricing for certain jobs, which refers basing the pay levels for a job directly on competitor organizations’ pay levels.
The market-review process consists of the following four steps.
Step 1: Choose Two or More Market-Survey Sources. No single market survey is ever perfect, as every market survey suffers from sampling and measurement error, some market surveys are conducting using more (or less) rigorous survey methodologies, and some market survey provide more breadth whereas others provide more depth. Given these reasons, we typically opt to gather data from at least two market-survey sources so that we don’t rely to heavily on a single flawed survey.
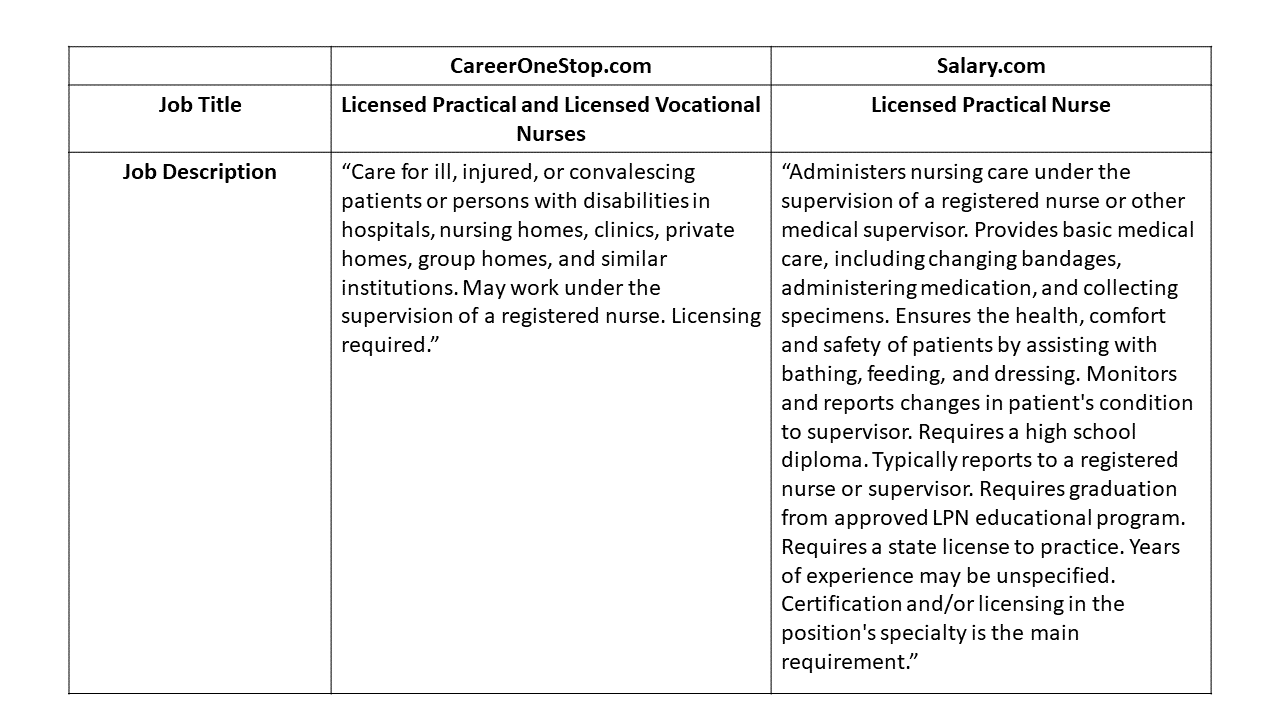
Step 2: Match the Job Descriptions. Often we won’t be able to find market survey data for every single job in our organization. Instead, we focus on what are called benchmark jobs (key jobs), which are jobs that are common within or across industries. For example, in the healthcare industry in the U.S., the job of a Registered Nurse would be considered a benchmark job, as most hospitals will employee at least one Registered Nurse and thus have pay data for that job. Once we’ve identified our benchmark jobs, we look through the market survey to see if we can find job title and/or job description matches. Even if the job title of our benchmark job differs from that of a benchmark job in the market survey, we can still potentially match the job based on the job description. This can be a tricky step, as the amount of information you have in your organization’s job description for the benchmark job in question may far exceed the amount of information in the market survey. Thus, using our subject matter expertise and knowledge of the job in question, we do our best to ensure that the market survey job is in fact equivalent or comparable to the job in our organization. As an example of how job titles and job descriptions in two market-survey sources can differ for what is essentially the same benchmark job, please refer to Table 1.
Step 3: Age the Survey Data. Different market surveys will collect pay data from organizations at different points in time, which means that the raw data from these surveys will often need to be aged to some date in the future. That is, often we wish to estimate the market pay rate of a benchmark job for some time point in the future. In doing so, we can make the survey data more up-to-date, consistent, and comparable across the market-survey sources we have access to. To do so, we need to determine the annual market movement rate (e.g., 3.1%) based on a budget growth projection, and using this information we can calculate what is referred to as an aging factor.
Step 4: Apply Survey Weights. Different market surveys are based on different sample sizes (e.g., number of organizations, number of employees), and as noted above, some market surveys are more rigorous from a methodological perspective. To account for sampling error, we can apply compute sample-weighted means (i.e., averages) in order to “weight” the survey data. In doing so, we can prioritize market pay data from market surveys based on larger sample sizes. Larger sample sizes are associated with lower sampling error, as they tend to me more representative of the underlying population from which the sample was drawn.
In the following sections, we will learn what it means to “age” market survey data and how we can apply market survey weights to the data. Doing so, allows us to make better judgments regarding the external competitiveness of an organization’s pay practices.
61.1.1 Aging Market Survey Data
Aging market survey (or pay) data refers to the process of “[identifying] when the pay data were originally collected and then [weighting] the data based on the expected change in the market pay rates resulting from merit-based increases, cost-of-living adjustments, and other factors that affect pay” (Bauer et al. 2025, 380–81). The process requires simple arithmetic and includes the following steps:
- Identify an appropriate annual wage/salary budget growth projection from a vendor like WorldatWork (e.g., 3.1% or .031).
- If the the budget growth projection from step 1 is an annual growth projection, then divide the value by 12 obtain a monthly value (e.g., .031 / 12 = .003).
- Determine how many months the data need to be aged (e.g., 7 months), multiply the value from step 2 by the number of months (e.g., .003 x 7 = .018), and given that growth is expected, add 1 to the product (e.g., .018 + 1 = 1.018) – the resulting value (e.g., 1.018) is the aging factor.
- Multiply each pay rate by the aging factor (e.g., 15.00 x 1.018 = 15.27) to age the data.
Given that different market survey sources might have been collected at different times, we may need to calculate and apply a different aging factor to each market survey source.
61.1.2 Applying Market Survey Weights
Applying market survey weights allows us to take into consideration the amount of sampling error (or lack thereof) in and/or level of rigor of different market survey sources. The process requires simple arithmetic and follows any aging of the data that was needed. We weight market survey data in different ways and for different reasons. For example, we could give greater weights to those surveys whose pay rate estimates were based on more employees or on more organizations. Alternatively, we could weight market survey data on the level of methodological rigor applied by the developer of the survey. In this chapter, we will calculate sample-weighted means based on the number of employees used to calculate the median hourly rate for a given job from a given survey; we could, however, have just as easily applied the same process but based on the number of organizations used to calculate the median hourly rate for a given job from a given survey.
61.1.3 Conceptual Video
For a more in-depth review of market surveys, please check out the following conceptual video.
Link to conceptual video: https://youtu.be/ey_QzvUIFyQ
61.2 Tutorial
This chapter’s tutorial demonstrates age market survey and apply market survey weights using R.
61.2.1 Video Tutorials
As usual, you have the choice to follow along with the written tutorial in this chapter or to watch the video tutorials below.
Link to video tutorial: https://youtu.be/RUWuiwV8PPE
Link to video tutorial: https://youtu.be/ixi7vozspUs
61.2.2 Functions & Packages Introduced
| Function | Package |
|---|---|
round |
base R |
View |
base R |
print |
base R |
function |
base R |
matrix |
base R |
nrow |
base R |
rowSums |
base R |
c |
base R |
61.2.3 Initial Steps
If you haven’t already, save the file called “MarketSurveyData.csv” into a folder that you will subsequently set as your working directory. Your working directory will likely be different than the one shown below (i.e., "H:/RWorkshop"). As a reminder, you can access all of the data files referenced in this book by downloading them as a compressed (zipped) folder from the my GitHub site: https://github.com/davidcaughlin/R-Tutorial-Data-Files; once you’ve followed the link to GitHub, just click “Code” (or “Download”) followed by “Download ZIP”, which will download all of the data files referenced in this book. For the sake of parsimony, I recommend downloading all of the data files into the same folder on your computer, which will allow you to set that same folder as your working directory for each of the chapters in this book.
Next, using the setwd function, set your working directory to the folder in which you saved the data file for this chapter. Alternatively, you can manually set your working directory folder in your drop-down menus by going to Session > Set Working Directory > Choose Directory…. Be sure to create a new R script file (.R) or update an existing R script file so that you can save your script and annotations. If you need refreshers on how to set your working directory and how to create and save an R script, please refer to Setting a Working Directory and Creating & Saving an R Script.
Next, read in the .csv data file called “MarketSurveyData.csv” using your choice of read function. In this example, I use the read_csv function from the readr package (Wickham, Hester, and Bryan 2024). If you choose to use the read_csv function, be sure that you have installed and accessed the readr package using the install.packages and library functions. Note: You don’t need to install a package every time you wish to access it; in general, I would recommend updating a package installation once ever 1-3 months. For refreshers on installing packages and reading data into R, please refer to Packages and Reading Data into R.
# Install readr package if you haven't already
# [Note: You don't need to install a package every
# time you wish to access it]
install.packages("readr")# Access readr package
library(readr)
# Read data and name data frame (tibble) object
md <- read_csv("MarketSurveyData.csv")## Rows: 6 Columns: 8
## ── Column specification ────────────────────────────────────────────────────────────────────────────────────────────────────────────
## Delimiter: ","
## chr (2): Job_ID, Job_Title
## dbl (6): Survey_1, Survey_2, Survey_3, SS_Survey_1, SS_Survey_2, SS_Survey_3
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.## [1] "Job_ID" "Job_Title" "Survey_1" "Survey_2" "Survey_3" "SS_Survey_1" "SS_Survey_2" "SS_Survey_3"## spc_tbl_ [6 × 8] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
## $ Job_ID : chr [1:6] "FE10" "FE12" "GE12" "GE13" ...
## $ Job_Title : chr [1:6] "Packaging Operator" "Machine Operator" "Electronics Assembler" "Coil Winder" ...
## $ Survey_1 : num [1:6] 14.1 15.9 15.7 16 19.4 ...
## $ Survey_2 : num [1:6] 14.5 15.8 15.8 15.5 20.1 ...
## $ Survey_3 : num [1:6] 14 16 15.3 16.1 19.8 ...
## $ SS_Survey_1: num [1:6] 101 88 90 56 26 32
## $ SS_Survey_2: num [1:6] 35 29 27 21 20 22
## $ SS_Survey_3: num [1:6] 13 11 11 6 4 4
## - attr(*, "spec")=
## .. cols(
## .. Job_ID = col_character(),
## .. Job_Title = col_character(),
## .. Survey_1 = col_double(),
## .. Survey_2 = col_double(),
## .. Survey_3 = col_double(),
## .. SS_Survey_1 = col_double(),
## .. SS_Survey_2 = col_double(),
## .. SS_Survey_3 = col_double()
## .. )
## - attr(*, "problems")=<externalptr>## # A tibble: 6 × 8
## Job_ID Job_Title Survey_1 Survey_2 Survey_3 SS_Survey_1 SS_Survey_2 SS_Survey_3
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 FE10 Packaging Operator 14.1 14.5 14.0 101 35 13
## 2 FE12 Machine Operator 15.9 15.8 16.0 88 29 11
## 3 GE12 Electronics Assembler 15.7 15.8 15.3 90 27 11
## 4 GE13 Coil Winder 16.0 15.5 16.1 56 21 6
## 5 GE14 Electronics Technician 19.4 20.1 19.8 26 20 4
## 6 IE08 Quality Assurance Technician 18.0 17.9 18.6 32 22 4## [1] 6There are 6 variables and 6 cases (i.e., jobs) in the md data frame: Job_ID, Job_Title, Survey_1, Survey_2, Survey_3, SS_Survey_1, SS_Survey_2, and SS_Survey_3. Per the output of the str (structure) function above, the Job_ID and Job_Titlevariables are of type character, and the other variables are of type numeric (continuous: interval/ratio). The Job_ID variable contains the unique identifiers for jobs, and the Job_Title variable contains the job titles. The three survey variables (Survey_1, Survey_2, Survey_3) include the median hourly pay rates for these jobs, all of which are nonexempt, from each of the three market survey sources used by the organization. The variables SS_Survey_1, SS_Survey_2, and SS_Survey_3 contain the number of employees used in each market survey source to estimate the median hourly pay rate for a given job.
61.2.4 Age the Data
To age the data from the first market survey (Survey_1), follow the following four steps.
Step One: To identify an appropriate annual wage/salary budget growth projection, we will use a reputable source (e.g., WorldatWork). For this tutorial, let’s assume that the annual wage/salary budget growth projection is 3.1% (i.e., .031). We’ll assign the budget growth projection value to an object called ABG (Annual Budget Growth) using the <- assignment operator.
Step Two: If the the budget growth projection from Step One is an annual growth projection (which it is in this case), then for Step Two, we will divide the value by 12 obtain a monthly value. Let’s assign the calculated monthly budget growth projection value to an object called MBG (Monthly Budget Growth) using the <- assignment operator.
Step Three: For this step, we will first determine how many months the data need to be aged. Let’s assume that the data for the first market survey (Survey_1) were estimated 6 months ago and that we want to age the data 1 month into the future. Given those assumptions, we need to age the market survey data by a total of 7 months (i.e., 6 + 1 = 7). Second, multiply the value from Step Two by the number of months that the data need to be aged. Third, given that growth is expected, add 1 to the product. The resulting value is the aging factor. Let’s assign the aging factor value to the object AF (aging factor).
Step Four: Let’s multiply each hourly pay rate from the first market survey (Survey_1) by the aging factor to age the data. We’ll create a new variable called Survey_1_aged and and assign the aged survey data to it using the <- assignment operator. Make sure to note that the Survey_1 variable and the new Survey_1_agedvariable belong to the md data frame by using the $ operator. As an optional follow-up step, use the round function from base R to round the values from the new Survey_1_agedvariable to two digits after the decimal.
# Step Four: Age the data
md$Survey_1_aged <- md$Survey_1 * AF
# Optional: Round the new variable to two digits after the decimal
md$Survey_1_aged <- round(md$Survey_1_aged, 2)Now that you have aged the data, take a look at the data frame object (md) to marvel at your work.
Alternatively, you can print the vector of sample-weighted means to your console.
## [1] 14.37 16.19 15.94 16.30 19.70 18.27Note: Given that different market survey sources might have been collected at different times, you may need to calculate and apply a different aging factor to each market survey source.
For the sake of brevity, let’s assume that the three market-survey sources all require the same aging factor (which likely won’t be the case in real life). We are doing this so that we can prepare to pass the aged data along to the next, phase in which we apply market-survey weights.
# Age remaining market survey data (with rounding to two digits)
md$Survey_2_aged <- round(md$Survey_2 * AF, 2)
md$Survey_3_aged <- round(md$Survey_3 * AF, 2)61.2.4.1 Optional: Age the Data with a Function
To streamline the four-step process from above, we can create our own function to age data. For example, we can create a function called age using function from base R. The script contained within the curly braces ({ }) essentially replicates what we did in the four-step process above. You don’t need to change anything in the script below – just run it as is.
# Optional: Create an aging function
age <- function(data, ABG, age_months) {
MBG <- ABG / 12
AF <- (MBG * age_months) + 1
round((data * AF), 2)
}Using the new age function, as the first argument, type data= followed by the name of data frame (md) followed by $ and the name of the market survey variable (Survey_1). As the second argument, type ABG= followed by the projected budget growth value (.031). As the third argument, type age_months followed by the number of months for which you would like to age the data. Use the <- assignment operator to assign the resulting values to a new variable (Survey_1_aged) to be added to your existing data frame (md).
# Age the market survey data
md$Survey_1_aged <- age(data=md$Survey_1, ABG=.031, age_months=7)
# Print vector of aged survey data
print(md$Survey_1_aged)## [1] 14.37 16.19 15.94 16.30 19.70 18.27Note: Given that different market survey sources might have been collected at different times, you may need to calculate and apply a different aging factor to each market survey source.
For the sake of brevity, let’s assume that the three market-survey sources all require the same aging factor (which likely won’t be the case in real life). We are doing this so that we can prepare to pass the aged data along to the next, phase in which we apply market-survey weights.
61.2.5 Compute the Sample-Weighted Means
After aging the data, we are ready to compute the sample-weighted means, which allows us to apply market survey weights to the data.
To compute the sample-weighted means for each job, first, we will multiply each job’s median hourly pay rate by the survey sample size on which its based, sum those products, and then divide that sum by the grand total of the sample sizes for all surveys used to estimate a job’s median hourly rate. This process gives us the sample-weighted mean for each job. Let’s use the <- assignment operator to assign the sample-weighted means to a new variable called Weighted_Mean that we will apply to our data frame (md). As a final step, let’s apply the round function from base R to round the values from the new Weighted_Meanvariable to two digits after the decimal.
# Compute sample-weighted means
md$Weighted_Mean <-
((md$Survey_1_aged * md$SS_Survey_1) + (md$Survey_2_aged * md$SS_Survey_2) + (md$Survey_3_aged * md$SS_Survey_3)) /
(md$SS_Survey_1 + md$SS_Survey_2 + md$SS_Survey_3)
# Optional: Round the new variable to two digits after the decimal
md$Weighted_Mean <- round(md$Weighted_Mean, 2)Now that we have computed sample-weighted means based on the median hourly pay rate for each job, take a look at the data frame verify that we performed this operation correctly.
Alternatively, you can print the vector of sample-weighted means to your console.
## [1] 14.45 16.19 15.94 16.18 20.05 18.2961.2.5.1 Optional: Compute the Sample-Weighted Means with a Function
If we wish to streamline the sample-weighted mean calculations from above, we can create our own function. For example, we can create a function called weighted.mean using function from base R. The script contained within the curly braces ({ }) replicates what we did above but uses matrix mathematics instead. You don’t need to change anything in the script below – just run it as is.
# Optional: Create a sample-weighted mean function
weighted.mean <- function(pay_rates, sample_sizes) {
a <- matrix(pay_rates, nrow=nrow(md))
b <- matrix(sample_sizes, nrow=nrow(md))
c <- a * b
d <- rowSums(c) / rowSums(b)
round(d, 2)
}Using the new weighted.mean function, as the first argument, we will type pay_rates= followed by the vector of market survey variables that contain the pay rate data from each market survey; be sure to include the name of the data frame (md) followed by $ and the name of the market survey variable (e.g., Survey_1) for each market survey variable. As the second argument, we will type sample_sizes= followed by the vector of sample size variables that contain the sample size data for each market survey, making sure to include the name of the data frame (md) followed by $ and the name of the sample size variable (e.g., SS_Survey_1). To create the aforementioned vectors, we will use the c function from base R. Use the <- assignment operator to assign the resulting values to a new variable (Weighted_Mean) to be added to your existing data frame (md).
# Calculate sample-weighted means
md$Weighted_Mean <- weighted.mean(pay_rates=c(md$Survey_1_aged, md$Survey_2_aged, md$Survey_3_aged),
sample_sizes=c(md$SS_Survey_1, md$SS_Survey_2, md$SS_Survey_3))
# Print vector of sample-weighted means
print(md$Weighted_Mean)## [1] 14.45 16.19 15.94 16.18 20.05 18.29